No CrossRef data available.
Published online by Cambridge University Press: 28 March 2014
Let C be a symmetric convex body of volume 1 in 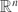 ${\mathbb R}^n$. We provide general estimates for the volume and the radius of C ∩ U(C) where U is a random orthogonal transformation of
${\mathbb R}^n$. We provide general estimates for the volume and the radius of C ∩ U(C) where U is a random orthogonal transformation of 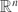 ${\mathbb R}^n$. In particular, we consider the case where C is in the isotropic position or C is the volume normalized Lq-centroid body Zq(μ) of an isotropic log-concave measure μ on
${\mathbb R}^n$. In particular, we consider the case where C is in the isotropic position or C is the volume normalized Lq-centroid body Zq(μ) of an isotropic log-concave measure μ on 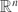 ${\mathbb R}^n$.
${\mathbb R}^n$.