On the converse of Mertens' theorem
Published online by Cambridge University Press: 24 October 2008
Extract
Let (λm), (µn) (m, n = 0, 1, 2,…) satisfy
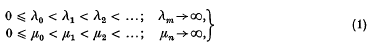
respectively. Let vp (p = 0, 1, 2, …) be the sequence (λm+µn) arranged in ascending order, equal sums λm+µn being considered as giving just one vp Then for given formal series Σam, Σbn the formal series C = Σ cp where
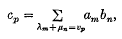
is called the general Dirichlet product of Σamand Σbn (see Hardy (2), p. 239). When λn = µn = n we have the Cauchy product. In the case λn = logm, µn = logn (m, n = 1, 2,…) we have vp =log p(p = 1, 2, …)and it is natural to call C the ordinary Dirichlet product.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 73 , Issue 3 , May 1973 , pp. 467 - 471
- Copyright
- Copyright © Cambridge Philosophical Society 1973
References
REFERENCES
- 2
- Cited by


