Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
van Wamelen, Paul
1997.
On the CM Character of the Curvesy2=xq−1.
Journal of Number Theory,
Vol. 64,
Issue. 1,
p.
59.
KIM, DAE-YEOUL
KOO, JA-KYUNG
and
KIM, MYUNG-HWAN
2005.
CONGRUENCE EQUATIONS OF axi+ byj≡ c AND axi+ byj+ dzt≡ c(modp) WHEN p=2q+1 WITH p AND q ODD PRIMES.
Communications of the Korean Mathematical Society,
Vol. 20,
Issue. 3,
p.
467.
Prasad, Dipendra
2019.
Contributions to algebraic number theory from India : From independence to late 90’s.
Indian Journal of Pure and Applied Mathematics,
Vol. 50,
Issue. 3,
p.
779.


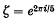 be a primitive fifth root of unity. Any element of
be a primitive fifth root of unity. Any element of 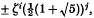 , with 0 ≤
, with 0 ≤ 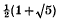 is the fundamental unit of the maximal real subfield
is the fundamental unit of the maximal real subfield 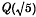 of
of 