On smoothing and differentiation of tables
Published online by Cambridge University Press: 24 October 2008
Extract
In recent seismological work several questions have arisen concerning the construction of tables from data containing a certain amount of accidental error, and it seems that some of the methods may be of more general interest. The first is the problem of smoothing. A method suggested by Dr L. J. Comrie was as follows. Suppose that we have values of y for five equally spaced values of x, and that we wish to make the second differences vary as smoothly as possible. We try to find a cubic polynomial such that the sum of the squares of the deviations of y from it will be a minimum. It is found that the polynomial is less than the observed value of y at the centre of the range by 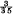 of the central fourth difference; or approximately by
of the central fourth difference; or approximately by 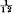 of the fourth difference. I have since found that the method had previously been suggested by Sir G. H. Darwin. It gives a great improvement in the steadiness of the differences and thereby makes interpolation much easier.
of the fourth difference. I have since found that the method had previously been suggested by Sir G. H. Darwin. It gives a great improvement in the steadiness of the differences and thereby makes interpolation much easier.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 30 , Issue 2 , 30 April 1934 , pp. 134 - 138
- Copyright
- Copyright © Cambridge Philosophical Society 1934
References
* Monthly Notice, Roy. Astron. Soc., Geophys. Suppl. 3 (1932), 10–13.Google Scholar
† Sci. Papers, 4, 298.
* In later work some systematic errors have been traced, but here the published values are given merely for illustration.
* Whittaker, and Robinson, , Calculus of Observations, 303–312.Google Scholar
- 2
- Cited by


