No CrossRef data available.
On sets of fractional dimensions
Published online by Cambridge University Press: 24 October 2008
Extract
1. Any number x can be expressed uniquely in the form
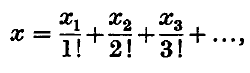
where the xr's are positive integers and where xr < r. In the present paper we consider the set of numbers Eb for which the xr's are bounded, so that 0 ≤ xr < b say, where b also is an integer. We prove that this set has dimension function
h(t) = b−u,
where t = euu−u−½(b − 1)(2π)−½, in the sense of Hausdorff.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 36 , Issue 2 , April 1940 , pp. 152 - 159
- Copyright
- Copyright © Cambridge Philosophical Society 1940
References
† Hausdorff, F., “Dimension und äusseres Mass". Math. Annalen, 79 (1919), 157–79.CrossRefGoogle Scholar
‡ A symbol like ![]() denotes summation over the members of the set I(E, ρ).
denotes summation over the members of the set I(E, ρ).
† Gillis, J., “Note on a theorem of Myrberg”, Proc. Cambridge Phil. Soc. 33 (1937), 420–4.CrossRefGoogle Scholar


