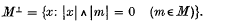Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Bokut’, L. A.
Zhevlakov, K. A.
and
Kuz’min, E. N.
1972.
Algebra and Geometry.
Vol. 12,
Issue. ,
p.
3.
1983.
Riesz Spaces II.
Vol. 30,
Issue. ,
p.
703.
Shamaev, I. I.
1987.
Abstract orthomorphisms and homomorphisms of lattice ordered algebras and their representations.
Siberian Mathematical Journal,
Vol. 28,
Issue. 1,
p.
166.
Bernau, S. J.
and
Huijsmans, C. B.
1989.
Ordered Algebraic Structures.
p.
175.
Bernau, S. J.
and
Huijsmans, C. B.
1990.
Almost f-algebras and d-algebras.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 107,
Issue. 2,
p.
287.
Huijsmans, Charles B.
1991.
Positive Operators, Riesz Spaces, and Economics.
Vol. 2,
Issue. ,
p.
151.
Henriksen, Melvin
1997.
Ordered Algebraic Structures.
p.
1.
Gargoubi, Hichem
and
Kossentini, Sayed
2016.
$${f}$$ f -Algebra Structure on Hyperbolic Numbers.
Advances in Applied Clifford Algebras,
Vol. 26,
Issue. 4,
p.
1211.
Kossentini, Sayed
2024.
Hypercomplex Representation of Finite-Dimensional Unital Archimedean f-Algebras.
Advances in Applied Clifford Algebras,
Vol. 34,
Issue. 4,