No CrossRef data available.
On Riemann summability of functions
Published online by Cambridge University Press: 24 October 2008
Extract
1. Let k be a positive integer. With the usual terminology, the series

will be said to be Riemann summable (R, k) to l if

converges for all sufficiently small x, and tends to l as x → 0. Here we take (sin nx)/(nx) as meaning 1 when n = 0. A more general summability method which has been considered by various authors ((1), (2), (5), (6), (8), (9), (10)), and is usually denoted by (ℜ, λ,k) is obtained by replacing (2) by
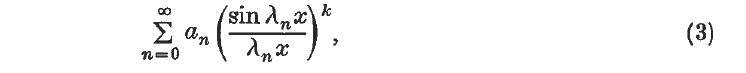
where λ = {λn} is a sequence of non-negative numbers increasing to ∞.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 75 , Issue 1 , January 1974 , pp. 83 - 94
- Copyright
- Copyright © Cambridge Philosophical Society 1974


