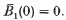Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-05T09:13:01.158Z Has data issue: false hasContentIssue false
  • English
  • Français

On reciprocity formulae for inhomogeneous and homogeneous Dedekind sums

Published online by Cambridge University Press:  24 October 2008

R. R. Hall  and
J. C. Wilson
R. R. Hall
Affiliation:
Department of Mathematics, University of York, York Y01 5DD
J. C. Wilson
Affiliation:
Department of Mathematics, University of York, York Y01 5DD
Get access Rights & Permissions [Opens in a new window]

Extract

A number of authors, including Apostol [1], Carlitz [2], Mikolás [5] and Rademacher [9] have obtained linear relations for the Dedekind sums

(the inhomogeneous sum) and the homogeneous sum

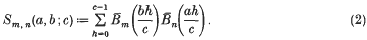
Here 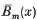denotes the periodic extension into ℝ of the Bernoulli polynomial Bm(X) on [0, 1] given by the relation

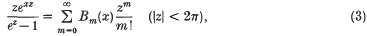
with the exception that we define

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 114 , Issue 1 , July 1993 , pp. 9 - 24
Copyright
Copyright © Cambridge Philosophical Society 1993

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Apostol, T. M.. Generalized Dedekind sums and the transformation formulae of certain Lambert series. Duke Math. J. 17 (1950), 147–157.CrossRefGoogle Scholar
[2]Carlitz, L.. Some theorems on generalized Dedekind sums. Pacific J.Math. 3 (1953), 513–522.CrossRefGoogle Scholar
[3]Greaves, G. R. H., Hall, R. R., Huxley, M. N. and Wilson, J. C.. Multiple Franel integrals. Mathematika, 40 (1993), 50–69.CrossRefGoogle Scholar
[4]Hall, R. R.. The distribution of squarefree numbers. J. reine angew Math. 394 (1989), 107–117.Google Scholar
[5]Mikolas, M.. On certain sums generating the Dedekind sums and their reciprocity laws. Pacific J. Math. 7 (1957), 1167–1178.CrossRefGoogle Scholar
[6]Montgomery, H. L. and Vaughan, R. C.. A basic inequality. In Gongreso de teoria de los numeros (Zarautz conf. proc.), ed. Aparicio, E., Calderon, C. and Peral, J. C. (1984).Google Scholar
[7]Montgomery, H. L. and Vaughan, R. C.. On the distribution of reduced residues. Annals of Math. 123 (1986), 311–333.CrossRefGoogle Scholar
[8]Rademacher, H.. Generalization of the reciprocity formula for Dedekind sums. Duke Math. J. 21 (1954), 391–397.CrossRefGoogle Scholar
[9]Rademacher, H. and Grosswald, E.. Dedekind Sums (Carus Math. Monographs, 16).Google Scholar