Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-24T02:41:24.610Z Has data issue: false hasContentIssue false
  • English
  • Français

On Positive Harmonic Functions in a Half-Plane

Published online by Cambridge University Press:  24 October 2008

S. Verblunsky
S. Verblunsky
Affiliation:
Magdalene College
Get access Rights & Permissions [Opens in a new window]

Extract

1. Let ξ, η denote the rectangular Cartesian coordinates of a point in a plane. Let J (ξ, η) denote a harmonic function which is positive in the half-plane η > 0. In this paper, we first show (Theorem I) that every such function J determines a non-negative number d, and a bounded non-diminishing function G(x), such that

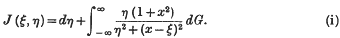
Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 31 , Issue 4 , October 1935 , pp. 482 - 507
Copyright
Copyright © Cambridge Philosophical Society 1935

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

* For further information concerning this case, see a paper by the author in Proc. London Math. Soc. (2), 37 (1934), 338–82Google Scholar, Theorem XXIV.

* Cf. Verblunsky, , Proc. London Math. Soc. (2), 38 (1934), 125–57Google Scholar, Theorem A.

* Hobson, , Theory of Functions of a Real Variable, 2, 246.Google Scholar

* Cf. Hardy, Littlewood and Pólya, , Inequalities (1934), pp. 196–8.Google Scholar

* Riesz, M.. Acta Math. 49 (1927), 465–97.CrossRefGoogle Scholar

* Cf. Zygmund, , Trigonometrical Series (1935), p. 48.Google Scholar

† Hardy, and Littlewood, , Journal London Math. Soc. 6 (1931), 281–6CrossRefGoogle Scholar, Theorem 1.

‡ Hardy, and Littlewood, , Journal London Math. Soc. 1 (1926), 134–8.CrossRefGoogle Scholar

* Hardy, Littlewood and Pólya, loc. cit. pp. 239, 246.

* Hardy, Littlewood and Pólya, loc. cit. 225, Theorem 346.