Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-26T07:52:36.705Z Has data issue: false hasContentIssue false
  • English
  • Français

On pairs of additive forms modulo one

Published online by Cambridge University Press:  24 October 2008

S. Schäffer
S. Schäffer
Affiliation:
Am Pastorenholz 8, 4972 Löhne, Germany
Get access Rights & Permissions [Opens in a new window]

Extract

Throughout this paper ∈ denotes an arbitrary positive number. For real α, ‖α‖ denotes the distance from α to the nearest integer. For natural numbers k we write K = 2k−1. In 1948 Heilbronn [8] showed that for any real α and N > C1(∈)

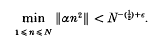
This theorem has since been generalized in many ways. In particular, results of the following type have been proved for natural numbers k ≥ 2, h = 1,2 and s.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 112 , Issue 3 , November 1992 , pp. 455 - 466
Copyright
Copyright © Cambridge Philosophical Society 1992

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Baker, R. C.. Diophantine Inequalities (Oxford University Press, 1986).Google Scholar
[2]Baker, R. C. and Gajraj, J.. On the fractional parts of certain additive forms. Math. Proc. Cambridge Philos. Soc. 79 (1976), 463–467.CrossRefGoogle Scholar
[3]Baker, R. C. and Harman, G.. Small fractional parts of quadratic and additive forms. Math. Proc. Cambridge Philos. Soc. 90 (1981), 5–12.CrossRefGoogle Scholar
[4]Baker, R. C. and Schäffer, S.. Pairs of additive quadratic forms modulo one. Acta Arith., to appear.Google Scholar
[5]Cook, R. J.. The fractional parts of an additive form. Proc. Cambridge Philos. Soc. 72 (1972), 209–212.CrossRefGoogle Scholar
[6]Danicic, I.. Contributions to number theory. Ph.D. thesis, University of London (1957).Google Scholar
[7]Davenport, H.. On a theorem of Heilbronn. Quart. J. Math. Oxford Ser. (2) 18 (1967), 339–344.CrossRefGoogle Scholar
[8]Heilbronn, H.. On the distribution of the sequence θn2 (mod 1). Quart. J. Math. Oxford Ser. (2) 19 (1948), 249–256.CrossRefGoogle Scholar
[9]Liu, M.-C.. On the fractional parts of θnk and ønk. Quart. J. Math. Oxford Ser. (2) 21 (1970), 481–486.CrossRefGoogle Scholar
[10]Liu, M.-C.. Simultaneous approximation of two additive forms. Proc. Cambridge Philos. Soc. 75 (1974), 77–82.CrossRefGoogle Scholar
[11]Schlickewei, H.-P.. On indefinite diagonal forms in many variables. J. Reine Angew. Math. 307/308 (1979), 279–294.Google Scholar
[12]Schmidt, W. M.. Small Fractional Parts of Polynomials. Regional Conference series no. 32 (American Mathematical Society. 1977).Google Scholar