Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-13T00:54:23.633Z Has data issue: false hasContentIssue false
  • English
  • Français

On nth roots and infinitely divisible elements in a connected Lie group

Published online by Cambridge University Press:  24 October 2008

M. McCrudden
M. McCrudden
Affiliation:
University of Manchester
Get access Rights & Permissions [Opens in a new window]

Extract

For any group G, x ∈ G and n ∈ ℕ (the natural numbers), let

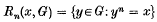
i.e. the set of all nth roots of x in G. If G is a Hausdorff topological group, then Rn(x, G) is a closed set in G, but may otherwise be quite complicated. However, as we have observed in (4), if G is a compact Lie group, then Rn(x, G) always has a finite number of connected components, and this result has led us to wonder about the connectedness properties of Rn(x, G) for other Lie groups G. Here is the result.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 89 , Issue 2 , March 1981 , pp. 293 - 299
Copyright
Copyright © Cambridge Philosophical Society 1981

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

(1)Borel, A. and Harish-Chandra, . Arithmetic subgroups of algebraic groups. Ann. of Math. Ser. 2, 75 (1962), 485–535.CrossRefGoogle Scholar
(2)Helgason, S.Differential Geometry and symmetric spaces (Academic Press, 1962).Google Scholar
(3)Hochschild, G.The structure of Lie groups (Holden-Day, San Francisco, 1965).Google Scholar
(4)McCrudden, M.On the nth root set of an element in a connected semisimple Lie group. Math.Proc. Cambridge Philos. Soc. 86 (1979), 219–225.CrossRefGoogle Scholar
(5)Mostow, G. D.On the fundamental group of a homogeneous space. Ann. of Math. 66 (1957), 249–255.CrossRefGoogle Scholar
(6)Steinberg, R.Conjugacy classes in algebraic groups. Lecture notes in mathematics no. 366 (Springer-Verlag, 1974).CrossRefGoogle Scholar
(7)Warner, G.Harmonic analysis on semisimple Lie groups vol. 1 (Springer-Verlag, 1972).Google Scholar