Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Oliveira, André G.
2015.
Torelli Theorem for the Moduli Spaces of Rank 2 Quadratic Pairs.
Communications in Algebra,
Vol. 43,
Issue. 8,
p.
3051.
Gukov, Sergei
Pei, Du
Yan, Wenbin
and
Ye, Ke
2018.
Equivariant Verlinde Algebra from Superconformal Index and Argyres–Seiberg Duality.
Communications in Mathematical Physics,
Vol. 357,
Issue. 3,
p.
1215.
Rayan, Steven
and
Sundbo, Evan
2018.
Twisted argyle quivers and Higgs bundles.
Bulletin des Sciences Mathématiques,
Vol. 146,
Issue. ,
p.
1.
Biswas, Indranil
Logares, Marina
and
Peón-Nieto, Ana
2021.
Symplectic Geometry of a Moduli Space of Framed Higgs Bundles.
International Mathematics Research Notices,
Vol. 2021,
Issue. 8,
p.
5623.
Kydonakis, Georgios
Sun, Hao
and
Zhao, Lutian
2021.
The Beauville-Narasimhan-Ramanan correspondence for twisted Higgs 𝑉-bundles and components of parabolic 𝑆𝑝(2𝑛,ℝ)-Higgs moduli spaces.
Transactions of the American Mathematical Society,
Vol. 374,
Issue. 6,
p.
4023.
Alfaya, David
and
Oliveira, André
2024.
Lie algebroid connections, twisted Higgs bundles and motives of moduli spaces.
Journal of Geometry and Physics,
Vol. 201,
Issue. ,
p.
105195.
Hu, Zhi
Huang, Pengfei
and
Zong, Runhong
2024.
Generalized Deligne–Hitchin twistor spaces: Construction and properties.
Bulletin des Sciences Mathématiques,
Vol. 191,
Issue. ,
p.
103396.
Biswas, Indranil
and
Singh, Anoop
2024.
Line bundles on the moduli space of Lie algebroid connections over a curve.
Bulletin des Sciences Mathématiques,
Vol. 193,
Issue. ,
p.
103421.
Roy, Sumit
2024.
On motives of parabolic Higgs bundles and parabolic connections.
Bulletin of Mathematical Sciences,
Vol. 14,
Issue. 02,
Alfaya, David
Biswas, Indranil
Gómez, Tomás L.
and
Mukhopadhyay, Swarnava
2025.
Torelli theorem for moduli stacks of vector bundles and principal G-bundles.
Journal of Geometry and Physics,
Vol. 207,
Issue. ,
p.
105350.


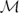 be the moduli space of Hitchin pairs (
be the moduli space of Hitchin pairs (
