Hostname: page-component-669899f699-cf6xr Total loading time: 0 Render date: 2025-04-26T00:25:17.872Z Has data issue: false hasContentIssue false
  • English
  • Français

On moduli of smoothness of k-monotone functions and applications

Published online by Cambridge University Press:  01 January 2009

KIRILL KOPOTUN
KIRILL KOPOTUN*
Affiliation:
Department of Mathematics, University of Manitoba, Winnipeg, Manitoba, R3T 2N2, Canada. e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 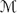k be the set of all k-monotone functions on (−1, 1), i.e., those functions f for which the kth divided differences [x0,. . ., xk; f] are nonnegative for all choices of (k+1) distinct points x0,. . .,xk in (−1, 1). We obtain estimates (which are exact in a certain sense) of kth Ditzian–Totik 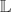q-moduli of smoothness of functions in 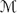k∩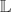p(−1, 1), where 1 ≤ q < p ≤ ∞, and discuss several applications of these estimates.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 146 , Issue 1 , January 2009 , pp. 213 - 223
Copyright
Copyright © Cambridge Philosophical Society 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

REFERENCES

[1]DeVore, R. A. and Lorentz, G. G.Constructive approximation. Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences] vol. 303 (Springer-Verlag, 1993).CrossRefGoogle Scholar
[2]Dyn, N., Lorentz, G. G. and Riemenschneider, S. D.Continuity of the birkhoff interpolation. SIAM J. Numer. Anal. 19 (1982), no. 3, 507–509.Google Scholar
[3]Ditzian, Z. and Totik, V.Moduli of smoothness. Springer Series in Computational Mathematics, vol. 9 (Springer-Verlag, 1987).Google Scholar
[4]Dzjadyk, V. K. Vvedenie v teoriyu ravnomernogo priblizheniya funktsii polinomami [introduction to the theory of uniform approximation of functions by polynomials]. Izdat. “Nauka”, Moscow (1977) (Russian).Google Scholar
[5]Ivanov, K. G.Direct and converse theorems for the best algebraic approximation in C[-1,1] and L p [-1,1]. C. R. Acad. Bulgare Sci. 33 (1980), no. 10, 1309–1312.Google Scholar
[6]Konovalov, V. N., Leviatan, D. and Maiorov, V. E. Approximation by polynomials and ridge functions of the classes of s-monotone radial functions, preprint.Google Scholar
[7]Kopotun, K. A.Whitney theorem of interpolatory type for k-monotone functions. Constr. Approx. 17 (2001), no. 2, 307–317.Google Scholar
[8]Kopotun, K. A.Approximation of k-monotone functions. J. Approx. Theory 94 (1998), no. 3, 481–493.Google Scholar
[9]Leviatan, D.Monotone and comonotone polynomial approximation revisited. J. Approx. Theory 53 (1988), no. 1, 1–16.CrossRefGoogle Scholar
[10]Nikoltjeva–Hedberg, M. and Operstein, V.A note on convex approximation in L p. J. Approx. Theory 81 (1995), no. 1, 141–144.CrossRefGoogle Scholar
[11]Pečarić, J. E., Proschan, F. and Tong, Y. L.Convex functions, partial orderings, and statistical applications. Math. Sci. Engrg. vol. 187 (Academic Press Inc., 1992).Google Scholar
[12]Roberts, A. W. and Varberg, D. E. Convex Functions (Academic Press, 1973), Pure and Appl. Math. vol. 57.Google Scholar
[13]Yu, X. M.Monotone polynomial approximation in L p space. Acta Math. Sinica (N.S.) 3 (1987), no. 4, 315–326.Google Scholar
[14]Yu, X. M.Convex polynomial approximation in L p space. Approx. Theory Appl. 3 (1987), 72–83.Google Scholar