Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-25T05:17:08.404Z Has data issue: false hasContentIssue false
  • English
  • Français

On Herschel's Condition and the Optical Cosine Law

Published online by Cambridge University Press:  24 October 2008

G. C. Steward
G. C. Steward
Affiliation:
Gonville and Caius College
Get access Rights & Permissions [Opens in a new window]

Extract

§ 1. Sir John Herschel gave the condition which must be satisfied in order that a symmetrical optical system, free from spherical aberration for two conjugate axial points, may also be free from spherical aberration for two neighbouring and conjugate points upon the axis of the system; but Herschel's condition applies only to first order aberration, i.e. to aberration depending upon the cube of the inclination of the ray to the axis. Abbe shewed, later, that this condition could be included in a wider result, viz. that the spherical aberration, supposed zero, is stationary for axial variations provided that the incident and emergent rays for two conjugate axial points, associated with modified magnification m, satisfy the relation

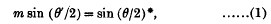
where θ and θ′ are their initial and final inclinations to the axis; and by ‘modified’ magnification is meant the ratio of the reduced sizes of the image and object.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 23 , Issue 6 , April 1927 , pp. 703 - 712
Copyright
Copyright © Cambridge Philosophical Society 1927

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

* See also a very elegant proof of these two conditions given by C., Hockin, J. R. Mic. Soc. (2), iv (1884).Google Scholar

† “The Aberrations of a Symmetrical Optical System,” Trans. Camb. Phil. Soc. IX, 1926Google Scholar; “Aberration Diffraction Effects,” Phil. Trans. Roy. Soc. A, 225, Part II, § 21.Google Scholar

* Smith, T., “The Optical Cosine Law,” Trans. Opt. Soc. Vol. xxiv (1922–1923), No. 1.Google Scholar

* Cf. Trans. Camb. Phil. Soc. IX, 1926, § 29 et seq.Google Scholar

* T., Smith, loc. cit.Google Scholar