In this note we consider a particular type of covering problem. Let T be given a plane set and Tθ be the set obtained from T by a rotation about some point in the plane through an angle θ in the clockwise sense. If a set K is such that for every θ there is a translation which transforms Tθ into a subset of K then we say that K is a rotation cover of T. The problem considered here is to determine for fixed n, l the triangle of least area which is a rotation cover for an n-sided regular polygon of side length l. In each case the solution is an equilateral triangle the altitude of which is given by

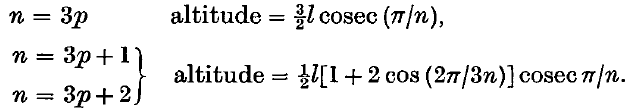
This solution is unique.