Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-26T07:32:54.510Z Has data issue: false hasContentIssue false
  • English
  • Français

On 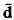-convergence of Markov chains

Published online by Cambridge University Press:  24 October 2008

D. J. Aldous
D. J. Aldous
Affiliation:
Department of Statistics, University of California, Berkeley, California 94720
Get access Rights & Permissions [Opens in a new window]

Extract

Let I be a countable set, with discrete topology, and let X = (Xn), Y = (Yn) be stationary stochastic processes taking values in I. To a probabilist, the natural topology on processes (strictly speaking, on distributions of processes) is weak convergence:

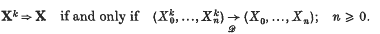
Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 90 , Issue 2 , September 1981 , pp. 331 - 333
Copyright
Copyright © Cambridge Philosophical Society 1981

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Ellis, M. H.Distances between two-state Markov processes attainable by Markov joinings. Trans. Amer. Math. Soc. 241 (1978), 129–153.CrossRefGoogle Scholar
(2)Ellis, M. H.On Kamae's conjecture concerning the d-distance between two-state Markov processes. Ann. Probability 8 (1980), 372–376.CrossRefGoogle Scholar
(3)Ellis, M. H.Conditions for attaining d by a Markovian joining. Ann. Probability 8 (1980), 431–440.CrossRefGoogle Scholar
(4)Ornstein, D. S.An application of ergodic theory to probability theory. Ann. Probability 1 (1973), 43–65.CrossRefGoogle Scholar