Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-20T09:13:02.949Z Has data issue: false hasContentIssue false
  • English
  • Français

On Appell's function F2

Published online by Cambridge University Press:  24 October 2008

H. L. Manocha
H. L. Manocha
Affiliation:
Department of Mathematics, Indian Institute of Technology, Delhi, India
Get access Rights & Permissions [Opens in a new window]

Extract

1. It has been observed that certain problems in quantum mechanics have their exact solutions which can be expressed in terms of Appell's function F2 as defined by (e.g. (7), p. 211)

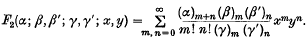
Having regard to this fact, Srivastava (5) proved a summation formula

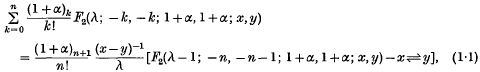
where R(λ) > 1, R(α) > − 1 and x⇌y indicates the presence on the right of a second term that originates from the first by interchanging x and y.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 65 , Issue 3 , May 1969 , pp. 687 - 689
Copyright
Copyright © Cambridge Philosophical Society 1969

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Erdélyi, A.Higher transcendental functions, vol. I (1953).Google Scholar
(2)Manocha, H. L. and Sharma, B. L.Some bilinear generating functions for Jacobi polynomials. Proc. Cambridge Philos. Soc. 63 (1967).Google Scholar
(3)Rainville, E. D.Special functions. New York (1960).Google Scholar
(4)Sharma, B. L.Integrals involving hypergeometric functions of two variables. Proc. Nat. Acad. Sci. India Sect. A (in the Press).Google Scholar
(5)Srivastava, H. M.On a summation formula for the Appell function F2. Proc. Cambridge Philos. Soc. 63 (1967), 1087–1089.CrossRefGoogle Scholar
(6)Slater, L. J.Confluent hypergeometric functions (Cambridge, 1960).Google Scholar
(7)Slater, L. J.Generalized hypergeometric functions (Cambridge, 1966).Google Scholar