Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-26T13:45:53.462Z Has data issue: false hasContentIssue false
  • English
  • Français

On an integral transform associated with a condition of radiation

Published online by Cambridge University Press:  24 October 2008

D. Naylor
D. Naylor
Affiliation:
University of Western Ontario
Get access Rights & Permissions [Opens in a new window]

Extract

1. There has been considerable debate on the conditions under which a given function f(r) can be expanded as a series of the orthogonal functions 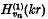where υ1, υ2, … are the zeros of the Hankel function 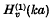regarded as a function of its order. Here k, a are positive constants and 0 < a ≤ r < ∞. The formal expansion can be written as

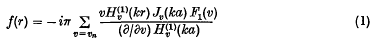
where

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 71 , Issue 2 , March 1972 , pp. 369 - 379
Copyright
Copyright © Cambridge Philosophical Society 1972

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Naylor, D.On an eigenfunction expansion associated with a condition of radiation. Proc. Cambridge Philos. Soc. 67 (1970), 107–121.CrossRefGoogle Scholar
(2)Magnus, W. & Kotin, I.The zeros of the Hankel function as a function of its order. Numer. Math. 2 (1960), 228–244.CrossRefGoogle Scholar
(3)Cochran, J. A.The zeros of Hankel functions as functions of their order. Numer. Math. 7 (1965), 238–250.CrossRefGoogle Scholar
(4)Keller, J. B., Rubinnow, S. I. & Goldstein, M.Zeros of Hankel functions and poles of scattering amplitudes. J. Mathematical Phys. 4 (1963), 829–832.CrossRefGoogle Scholar
(5)Pflumm, E.Expansion problems arising from the Watson transformation. (New YorkUniversity, Division of Electromagnetic Research, Report BR 35, 1960.)Google Scholar
(6)Cohen, D. S.Eigenfunction expansions and non-self adjoint boundary value problems. Comm. Pure Appl. Math. 17 (1964), 23–34.CrossRefGoogle Scholar
(7)Chakrabarti, A.Derivation of certain finite Kontorovitch type of integral transforms. Studia Sci. Math. Hungar. 4 (1969), 45–53.Google Scholar
(8)Marcenko, V. A.Expansion in Eigenfunctions of non-self-adjoint singular differential operators of second order. American Math. Soc. Trans. 2 (25), 77–130 (1963). Mat. Sb. 52 (94), (1960), 739–788.Google Scholar
(9)Watson, G. N.Theory of Bessel functions, Second Edition (Cambridge University Press, 1958).Google Scholar
(10)Duff, G. F. D. & Naylor, D.Differential equations of applied mathematics (John Wiley and Sons Inc., 1966).Google Scholar