Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-26T07:27:06.475Z Has data issue: false hasContentIssue false
  • English
  • Français

On a Genetics Model of Moran†

Published online by Cambridge University Press:  24 October 2008

Samuel Karlin  and
James McGregor
Samuel Karlin
Affiliation:
Applied Mathematics and Statistics LaboratoriesStanford UniversityStanfordCalifornia
James McGregor
Affiliation:
Applied Mathematics and Statistics LaboratoriesStanford UniversityStanfordCalifornia
Get access Rights & Permissions [Opens in a new window]

Extract

Wright (14), Feller (2) and others have proposed various stochastic models of genetics to study the fluctuations of gene frequency under the influence of mutation and selection. One of their simplest models has the following structure. There are a fixed number N of gametes each of which may be of two types a or A. The process X(n), n = 0, 1, 2, … which is assumed to have stationary transitions, is said to be in state j when there are j gametes of type a, and N − j of type A. Let γ1 denote the probability that immediately after formation an a gamete mutates into an A gamete and let γ2 denote the probability of an A gamete mutating into an a gamete. Each of the gametes of the next generation is independently formed by making a random selection from the gametes of the present generation. 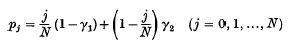The probability of a particular gamete in the next generation being of type a is then and of type A 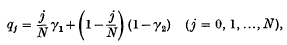where j represents the state of the process. Roughly speaking, the chance of a mating resulting in a gamete of a prescribed kind for the next generation is proportional to the fraction of these gametes present in this generation allowing for mutation effects.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 58 , Issue 2 , April 1962 , pp. 299 - 311
Copyright
Copyright © Cambridge Philosophical Society 1962

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Erdéelyi, A. (ed.). Higher transcendental functions, vol. II (New York, 1953).Google Scholar
(2)Feller, W. Diffusion processes in genetics. Proc. Second Berkeley Symposium on Mathematical Statistics and Probability (Berkeley, 1951), 227–246.Google Scholar
(3)Karlin, S.Total positivity, absorption probabilities and applications. Bull. American Math. Soc. 67 (1961), 105–108.CrossRefGoogle Scholar
(4)Karlin, S. and McGregor, J. L.The differential equations of birth and death processes and the Stieltjes moment problem. Trans. American Math. Soc. 85 (1957), 489–546.CrossRefGoogle Scholar
(5)Karlin, S. and Mcgregor, J. L.The classication of birth and death processes. Trans. American Math. Soc. 86 (1957), 366–400.CrossRefGoogle Scholar
(6)Karlin, S. and Mcgregor, J. L.A characterization of the birth and death process. Proc. Nat. Acad. Sci., U.S.A. 45 (1959), 375–379.CrossRefGoogle Scholar
(7)Karlin, S. and Mcgregor, J. L.Classical diffusion processes and total positivity. J. Math. Analysis and Applications, 1 (1960), 163–183.CrossRefGoogle Scholar
(8)Karlin, S. and Mcgregor, J. L.The Hahn polynomials, formulas and an application. Scripta Math. 26 (1961), 33–46.Google Scholar
(9)Kimura, M.Some problems of stochastic processes in genetics. Ann. Math. Statist. 28 (1957), 882–901.CrossRefGoogle Scholar
(10)Moran, P. A. P.Random processes in genetics. Proc. Cambridge Philos. Soc. 54 (1958), 60–72.CrossRefGoogle Scholar
(11)Moran, P. A. P.The effect of selection in a haploid genetic population. Proc. Cambridge Philos. Soc. 54 (1958), 463–467.CrossRefGoogle Scholar
(12)Moran, P. A. P.The distribution of gene frequency in a bisexual diploid population. Proc. Cambridge Philos. Soc. 54 (1958), 468–474.CrossRefGoogle Scholar
(13)Moran, P. A. P.A general theory of the distribution of gene frequencies. I. Overlapping generations. Proc. Roy. Soc. London. Ser. B, 149 (1958), 102–112.Google ScholarPubMed
(14)Wright, S.The genetical structure of populations. Ann. Eugenics, 15 (1951), 323–354.CrossRefGoogle ScholarPubMed