Hostname: page-component-78c5997874-s2hrs Total loading time: 0 Render date: 2024-11-09T13:34:04.783Z Has data issue: false hasContentIssue false
  • English
  • Français

On a conjecture of Mordell concerning binary cubic forms

Published online by Cambridge University Press:  24 October 2008

H. Davenport
H. Davenport
Affiliation:
The UniversityManchester 13
Get access Rights & Permissions [Opens in a new window]

Extract

Let f(x, y) be a binary cubic form with real coefficients and determinant D ≠ 0. In a recent paper, Mordell has proved that there exist integral values of x, y, not both zero, for which

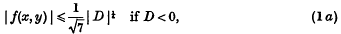
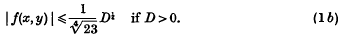
These inequalities are best possible, since they cannot be satisfied with the sign of strict inequality when f(x, y) is equivalent to

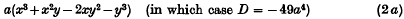
for the case D < 0, or to

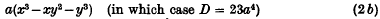
for the case D > 0.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 37 , Issue 4 , October 1941 , pp. 325 - 330
Copyright
Copyright © Cambridge Philosophical Society 1941

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

* The determinant of ax 3 + bx 2y + cxy 2 + dy 3 is the invariant

† Proc. London Math. Soc. (in course of publication).

* Proc. London Math. Soc. (2), 44 (1938), 412–31Google Scholar, and 45 (1939), 98–125.

* For references, see Koksma, , Diophantische Approximationen, p. 55Google Scholar. A much weaker result would suffice for the argument.

* See, for example, Perron, Kettenbrüchen, Kapitel 2, Satz 16.