Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-29T19:16:37.818Z Has data issue: false hasContentIssue false
  • English
  • Français

Obstructions for semigroups of partial isometries to be self-adjoint†

Published online by Cambridge University Press:  10 March 2016

JANEZ BERNIK  and
ALEXEY I. POPOV
JANEZ BERNIK
Affiliation:
Fakulteta za Matematiko in Fiziko, Univerza v Ljubljani, Jadranska 19, 1000 Ljubljana, Slovenia. e-mail: [email protected]
ALEXEY I. POPOV
Affiliation:
Department of Mathematics and Computer Science, Univresity of Lethbridge, C526 University Hall, 4401 University Drive, Lethbridge, Alberta T1K 3M4, Canada. e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we study the following question: given a semigroup ${\mathcal S}$ of partial isometries acting on a complex separable Hilbert space, when does the selfadjoint semigroup 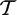${\mathcal T}$ generated by ${\mathcal S}$ again consist of partial isometries? It has been shown by Bernik, Marcoux, Popov and Radjavi that the answer is positive if the von Neumann algebra generated by the initial and final projections corresponding to the members of ${\mathcal S}$ is abelian and has finite multiplicity. In this paper we study the remaining case of when this von Neumann algebra has infinite multiplicity and show that, in a sense, the answer in this case is generically negative.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 161 , Issue 1 , July 2016 , pp. 107 - 116
Copyright
Copyright © Cambridge Philosophical Society 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

†

Research supported in part by ARRS (Slovenia)

References

REFERENCES

[1]Bernik, J., Marcoux, L. W., Popov, A. I. and Radjavi, H. On selfadjoint extensions of semigroups of partial isometries. Tran. Amer. Math. Soc., in press.Google Scholar
[2]Davidson, K. R.C*-algebras by example. Fields Institute Monographs, 6. (American Mathematical Society, Providence, RI, 1996).CrossRefGoogle Scholar
[3]Dixmier, J.von Neumann algebras. With a preface by Lance, E. C. Translated from the second French edition by Jellett, F. North-Holland Mathematical Library, 27 (North-Holland Publishing Co., Amsterdam-New York, 1981).Google Scholar
[4]Duncan, J. and Paterson, A. L. T.C*-algebras of inverse semigroups. Proc. Edinburgh Math. Soc. 28 1985, 41–58.CrossRefGoogle Scholar
[5]Halmos, P. R. and Wallen, L. J.Powers of partial isometries. J. Math. Mechanics 19, No. 8 (1970).Google Scholar
[6]Howie, J. M.Fundamentals of Semigroup Theory. London Math. Soc. Monogr. New Series (Clarendon Press, Oxford, 1985).Google Scholar
[7]Kadison, R. and Ringrose, J.Fundamentals of the theory of Operator Algebras, vol. II. Advanced theory. Pure Appl. Math. 100 (Academic Press, Inc., Orlando, FL, 1986).Google Scholar
[8]Petrich, M.Inverse Semigroups. Pure and Applied Mathematics (John Wiley and Sons, New York, 1984).Google Scholar
[9]Popov, A. I.On matrix semigroups bounded above and below. Linear Algebra Appl. 438 (2013), 4439–4447.CrossRefGoogle Scholar
[10]Popov, A. I. and Radjavi, H.Semigroups of partial isometries. Semigroup Forum. 87, Issue 3 (2013), Pp. 663–678.CrossRefGoogle Scholar