Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-26T07:33:16.108Z Has data issue: false hasContentIssue false
  • English
  • Français

The numerical calculation of

Published online by Cambridge University Press:  24 October 2008

D. Burnett
D. Burnett
Affiliation:
Clare College
Get access Rights & Permissions [Opens in a new window]

Extract

The type of integral considered, 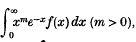is of frequent occurrence in problems in the kinetic theory of gases and in particular is required in the paper which follows, in calculating viscosity. The result is an extension of one given by Berger, and the analysis follows closely the discussion of Gauss's formula for approximate quadrature in Whittaker and Robinson, The calculus of observations; the novelty lies in the use of Sonine polynomials, which are peculiarly well suited for the discussion of this type of integral.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 33 , Issue 3 , July 1937 , pp. 359 - 362
Copyright
Copyright © Cambridge Philosophical Society 1937

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

* Berger, , Nova Acta Upsaliensis (3), 16 (1893).Google Scholar

† These are effectively the same polynomials as are used by Schrödinger in his wellknown papers on wave mechanics under the name of generalized Laguerre polynomials; but I have preferred to follow the nomenclature and notation of earlier authors—cf. for example Whittaker, and Watson, , Modern analysis, 4th ed. (Cambridge, 1927), p. 352,Google Scholar ex. 8, and Bateman, , Electrical and optical wave motion (Cambridge, 1915), 98.Google Scholar

‡ Cf. Burnett, , Proc. Lond. Math. Soc. (2), 39 (1935), 385.CrossRefGoogle Scholar

* This case is trivial but is given for completeness and to illustrate the method.

* Cf. Chapman, , Phil. Trans. Roy. Soc. 211 (1911), 433;CrossRefGoogle ScholarMassey, and Mohr, , Proc. Roy. Soc. 141 (1933), 434.CrossRefGoogle Scholar