Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-24T03:37:14.742Z Has data issue: false hasContentIssue false
  • English
  • Français

The number of apparent double points of certain loci

Published online by Cambridge University Press:  24 October 2008

W. L. Edge
W. L. Edge
Affiliation:
Trinity College
Get access Rights & Permissions [Opens in a new window]

Extract

1. A sketch of the first part of this paper, together with some of the second part, was first written out in October last, shortly after the publication of Mr Babbage's paper, A series of rational loci with one apparent double point. It is well known that the Del Pezzo quintic surface 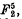the only non-ruled quintic surface in [5], has one apparent double point; Babbage shows that this surface is a member of a series of loci 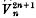in [2n + 1], each of which has one apparent double point; he establishes the existence of these loci from their representations on flat spaces ∑n, these representations being analogous to the plane representation of 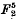by means of cubic curves through four fixed points.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 28 , Issue 3 , July 1932 , pp. 285 - 299
Copyright
Copyright © Cambridge Philosophical Society 1932

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

* Babbage, , Proc. Camb. Phil. Soc., 27 (1931), 399.CrossRefGoogle Scholar

† Severi, , Palermo Rendiconti, 15 (1901), 33–51 (44).CrossRefGoogle Scholar

* Baker, , “Note in regard to surfaces in space of four dimensions, in particular rational surfaces”, Proc. Camb. Phil. Soc., 28 (1932), 62–82.CrossRefGoogle Scholar

† Mr Babbage has written a note on this second series of loci , the manuscript of which he has shown to me. He uses an induction argument to prove that has one apparent double point.

* This locus is rational and represented on [3] by means of cubic surfaces through an elliptic quartic curve; it is studied from this point of view by Semple, , Proc. Camb. Phil. Soc., 25 (1929), 158CrossRefGoogle Scholar.

* Segre, , “Sulle rigate razionali in uno spazio lineare qualunque”, Atti Torino, 19 (1884), 355–372 (360).Google Scholar

* Cf. Segre, , “Sulle rigate razionali in uno spazio lineare qualunque”, Atti Torino, 19 (1884), 355–372 (371).Google Scholar

* The projection of this surface from a point on to [4] figures in a recent paper by Semple, , Proc. Lond. Math. Soc., 32 (1931), 388–9.Google Scholar

† The genus of a curve of order μ which lies on a cubic scroll in [4] and meets each generator in k points is . See, for example, Edge, , The theory of ruled surfaces (Cambridge 1931), 15.Google Scholar

* I is a relative invariant for birational transformation. If two surfaces are birationally equivalent there is in general a certain number of fundamental points on each surface, i.e. points to each of which there correspond, in the birational correspondence, all the points of a curve on the other surface. If the values of the Zeuthen-Segre invariant for the two surfaces are I and I′ while the numbers of fundamental points are f and f′ respectively, then I + f = I′ + f′.

* Baker, loc. cit., 76.

† The condition that a plane cubic should have a double point is that its discriminant should vanish; and this discriminant is of degree 12 in the coefficients.