Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-27T02:37:47.085Z Has data issue: false hasContentIssue false
  • English
  • Français

Notes on the theory of series (XXIV): a curious power-series

Published online by Cambridge University Press:  24 October 2008

G. H. Hardy  and
J. E. Littlewood
G. H. Hardy
Affiliation:
Trinity CollegeCambridge
J. E. Littlewood
Affiliation:
Trinity CollegeCambridge
Get access Rights & Permissions [Opens in a new window]

Extract

1. This note originates from a question put to us by Mr W. R. Dean concerning series of the type

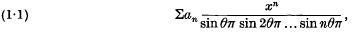
where θ is irrational. Series of the type

are familiar: it is well known, for example, that

may have any radius of convergence from 0 to 1 inclusive, according to the arithmetic nature of θ. It is natural to ask how this radius is connected with that of

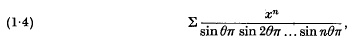
and, more generally, how those of (1·1) and (1·2) are connected.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 42 , Issue 2 , June 1946 , pp. 85 - 90
Copyright
Copyright © Cambridge Philosophical Society 1946

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

* See Proc. Cambridge Phil. Soc. 42 (1946), 24.Google Scholar The actual series encountered by Dean was

* The identity (2·3) is naturally not a new one, though we cannot refer to a quite explicit statement of it. The expression of F(x, q) as an infinite product goes back to Euler (see for example Macmahon, Combinatory analysis, vol. 2, 2), and the transformation in (2·4) is one of a type familiar in the theory of elliptic functions.

† For which does not exceed 16 if Actually the best value of A is 2.

* See for example Harkness, and Morley, , Introduction to the theory of analytic functions, 134–6.Google Scholar The theorem is stated there in the form in which the coefficients depend on an integral parameter m which tends to infinity (‘Weierstrass's double series theorem’).

Alternatively, we may appeal to the representation of C n(q) as an integral by means of Cauchy's theorem.

* By a well-known theorem of Bohl, Sierpinski and Weyl: see Weyl, , Math. Annalen, 77 (1916), 313–52CrossRefGoogle Scholar (314), or Hardy, and Wright, , Introduction to the theory of numbers, 378–81.Google Scholar

† Except Theorem 5, which refers to a special class of θ.

‡ By another theorem of Weyl, substantially equivalent to the theorem of uniform distribution already quoted.

* See for example, Hardy and Wright, 168.