No CrossRef data available.
Note on the Theory of Measure
Published online by Cambridge University Press: 24 October 2008
Extract
A function of sets γ(E) absolutely additive is termed by Radonée Poussin continuous if γ(E) vanishes whenever E consists of a single point only. It is known that if a function of sets 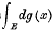 is not continuous there exists a countable set ε1 and a continuous function of sets
is not continuous there exists a countable set ε1 and a continuous function of sets 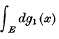 such that
such that
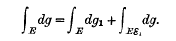
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 26 , Issue 1 , January 1930 , pp. 88 - 93
- Copyright
- Copyright © Cambridge Philosophical Society 1930
References
* This means that for sets Ei without common points (i = 1, …, ∞) the equation ![]() is valid and its left-hand side is absolutely convergent.
is valid and its left-hand side is absolutely convergent.
† “Absolut additive Mengenfunktionen,” Wiener Sitzungsber. 122 (a) (1913) p. 1351.Google Scholar
‡ Integrates de Lebesgue (Collection Borel; Paris 1916) p. 57.Google Scholar
§ Every absolutely additive function of sets defined for all Borel sets is known to be of the form ![]() , where g(x) is of bounded variation. The symbol x stands as usual for the ensemble of the coordinates of a variable point in space of a finite number of dimensions.
, where g(x) is of bounded variation. The symbol x stands as usual for the ensemble of the coordinates of a variable point in space of a finite number of dimensions.
* A portion of a set E is the common part of E with an open interval Δ, together with any limiting points of (E. Δ) which are points of E. The portion is only regarded as existing when this common part is not “empty”.
† The function equal to 1 in H and to 0 outside H.
‡ I.e. of one of Baire's classes.
§ See Cantor, G., Math. Annalen 23 (1886) pp. 453–488.CrossRefGoogle Scholar
∥ The black intervals of a linear closed set H are the open intervals non-overlapping whose sum constitutes the complement of the closed set H.
* A system of sets σ is everywhere dense on a set H if every interval Δ containing a portion of H also contains a set E of the system σ with a point of H in that set E. This notation, which does not seem to have been used before, simplifies the language very much in investigations relating to portions of sets. Denjoy, , in his memoir “Sur les nombres dérivés des fonctions continues,” Journal de Hath. (7) 1, fasc. II (1915) pp. 105 seq., constantly uses systems of sets of this kind.Google Scholar
* We use the notation ![]() to mean
to mean ![]() where z the ensemble (x, y) and g(z) the indefinite integral of g 1(x, y) with respect to g 2(y). It can be shown that
where z the ensemble (x, y) and g(z) the indefinite integral of g 1(x, y) with respect to g 2(y). It can be shown that
when the left-hand side is absolutely convergent. This is the generalised form of the equality of multiple and repeated integrals. These things will be explained in detail in a further paper.
* We give the name Stieltjes Transformation to the formula
This formula is valid whenever one side exists, the product f. φ being taken as meaning zero whenever it has an indeterminate form. The Stieltjes Transformation like the equality of multiple and repeated integrals is studied in detail in the paper already referred to, which I hope to complete soon.
† Alexandroff, , Comptes Rendus, 162 (1916) p. 323.Google Scholar
* This is especially the case in the theory of derivation, e.g. “The points at which f + and f − are finite and f + > f − form a set of measure zero; those at which f + < f − form a countable see” young, G. C., proc. London Math. Soc. (2) 15 (1916) p. 360.Google Scholar
† A function f(x) denned in a set E and finite in E, measurable with respect to g(x), is continuous over a closed subset of E having g-content arbitrarily near to that of E.
‡ By a result of Denjoy, : Annales de l'Ècole normale (3) 33 (1916) p. 143.Google Scholar


