Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-23T11:15:29.574Z Has data issue: false hasContentIssue false
  • English
  • Français

Note on the invariant of plane cubics

Published online by Cambridge University Press:  24 October 2008

C. T. C. Wall
C. T. C. Wall
Affiliation:
University of Liverpool
Get access Rights & Permissions [Opens in a new window]

Extract

It was noted by Klein(4), part I, ch. II, §9, that if a polyhedral group G acts on the 2-sphere identified with P1(ℂ), then the polynomials cΠg∈G(λ − ag μ) form, as a∈ℂ varies, a vector space of dimension 2 over ℂ. G is generated by elements T1, T2 fixing respectively a vertex and a face; T1T2 fixes an edge and these elements have orders p, q, 2 where 1/p + 1/q > ½ Taking a to be a vertex or the mid-point of a face or an edge yields polynomials of the form 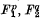and 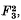which are thus linearly dependent. The ring of all (relatively) invariant polynomials is generated by F1F2 and F3 subject to this single relation.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 85 , Issue 3 , May 1979 , pp. 403 - 406
Copyright
Copyright © Cambridge Philosophical Society 1979

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Cayley, A.A third memoir on quantics. Phil. Trans. Roy. Soc. 146, (1856), 627–647.Google Scholar
(2)Coxeter, H. S. M. and Moser, W.Generators and relations for discrete groups, 2nd ed. (Berlin, Göttingen, Heidelberg, Springer-Verlag, 1957).CrossRefGoogle Scholar
(3)Enriques, F.Teoria geometrica delle equazioni, vol. II. (Bologna, Nicola Zanichelli, c. 1900).Google Scholar
(4)Klein, F.Lectures on the Icosahedron (1884, translated into English 1888, republished by Dover 1956).Google Scholar
(5)Klein, F. & Fricke, R.Theorie der elliptischen Modulfunktionen, vol. I (Leipzig, B. G. Teubner, 1890).Google Scholar
(6)Salmon, G.Higher plane curves, 3rd ed. (Dublin, 1879).Google Scholar