Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-29T18:56:54.947Z Has data issue: false hasContentIssue false
  • English
  • Français

Note on the generalized Mehler transform

Published online by Cambridge University Press:  24 October 2008

J. S. Lowndes
J. S. Lowndes
Affiliation:
Royal College of Science and Technology, Glasgow
Get access Rights & Permissions [Opens in a new window]

Extract

1. The integral transform. One result of recent studies of boundary-value problems of the wave and diffusion equations involving wedge- or conically-shaped boundaries has been the interest shown in integrals in which the variable of integration appears as the order of Bessel or Legendre functions. An integral of this type occurs as the inversion formula for the generalized Mehler transform which is defined by

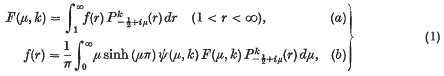
where ψ(μ, k) = Γ(½ − k + iμ)Γ(½ − k − iμ) and 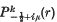is the associated Legendre function of the first kind. Oberhettinger and Higgins (4) have given a table of transform pairs corresponding to the above transform.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 60 , Issue 1 , January 1964 , pp. 57 - 59
Copyright
Copyright © Cambridge Philosophical Society 1964

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Erdélyi, A., Magnus, W., Oberhettinger, F. and Tricomi, F. G.Higher transcendental functions, Vol. 2 (McGraw-Hill, 1953).Google Scholar
(2)Lebedev, N. N.Dokl. Akad. Nauk, SSSR, 68 (1949), 653–656Google Scholar
(3)Lowndes, J. S.SIAM Rev. 3 (1961), 162–164CrossRefGoogle Scholar
(4)Oberhettinger, F. and Higgins, T. P.Tables of Lebedev, Mehler and generalized Mehler Transforms (Boeing Scientific Research Laboratories Mathematical Note 246; Washington, 1961).CrossRefGoogle Scholar