Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-26T13:49:22.087Z Has data issue: false hasContentIssue false
  • English
  • Français

A note on the Fourier transform of generalized functions

Published online by Cambridge University Press:  24 October 2008

B. Fisher
B. Fisher
Affiliation:
University of Leicester
Get access Rights & Permissions [Opens in a new window]

Extract

If F(f) denotes the Fourier transform of a generalized function f and f * g denotes the convolution product of two generalized functions f and g then it is known that under certain conditions

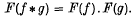
Jones (2) states that this is not true in general and gives as a counter-example the case when f = g = H, H denoting Heaviside's function. In this case

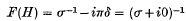
and the product (x−1 – iπδ)2 is not defined in his development of the product of generalized functions.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 70 , Issue 1 , July 1971 , pp. 49 - 51
Copyright
Copyright © Cambridge Philosophical Society 1971

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Fisher, B.The generalized function (x + i0)λ. Proc. Cambridge Philoe. Soc. 68 (1970), 707.CrossRefGoogle Scholar
(2)Jones, D. S.Generalised functions (McGraw-Hill, 1966).Google Scholar