Published online by Cambridge University Press: 24 October 2008
A square matrix A, of order n, having complex coefficients can be inverted without the aid of any operations involving complex numbers. This can be done if the coefficients ars + iαrs are replaced by their matrix equivalents 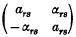 and the resulting 2n × 2n real matrix A1 is inverted. The inverse will be a 2n × 2n matrix of similar form in which the subsidiary 2 × 2 matrices can be replaced by the equivalent complex numbers, thus yielding the inverse of A. It is the purpose of this note to show that a similar technique can be employed to evaluate det A.
and the resulting 2n × 2n real matrix A1 is inverted. The inverse will be a 2n × 2n matrix of similar form in which the subsidiary 2 × 2 matrices can be replaced by the equivalent complex numbers, thus yielding the inverse of A. It is the purpose of this note to show that a similar technique can be employed to evaluate det A.
* See, for example, Frazer, , Duncan, and Collar, , Elementary matrices (Cambridge, 1938), p. 35.CrossRefGoogle Scholar
† For a detailed computational layout of the process of triangular resolution see Fox, L., ‘Practical methods for the solution of linear equations and the inversion of matrices’, J.R. Statist. Soc. (in the Press).Google Scholar