A note on system normalizers of a finite soluble group
Published online by Cambridge University Press: 24 October 2008
Extract
Introduction. Hall ((3), (4)) introduced the concept of a Sylow system and its normalizer into the theory of finite soluble groups. In (4) he showed that system normalizers may be characterized as those subgroups D of G minimal subject to the existence of a chain of subgroups from D up to G in which each subgroup is maximal and non-normal in the next; he also showed that a system normalizer covers all the central chief factors and avoids all the eccentric chief factors of G (for definitions of covering and avoidance, and an account of their elementary properties), the reader is referred to Taunt ((5)). This note arises out of an investigation into the question to what extent this covering/ avoidance property characterizes system normalizers; it provides a partial answer by means of two elementary counter-examples given in section 3 which seem to indicate that the property ceases to characterize system normalizers as soon as the ‘non-commutativity’ of the group is increased beyond a certain threshold. For the sake of completeness we include proofs in Theorems 1 and 2 of generalizations of two known results communicated to me by Dr Taunt and which as far as we know have not been published elsewhere. Theorem 1 shows the covering/avoidance property to be characteristic for the class 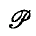 of soluble groups with self-normalizing system normalizers introduced by Carter in (1), while Theorem 2 shows the same is true for A -groups (soluble groups with Abelian Sylow subgroups investigated by Taunt in (5)).
of soluble groups with self-normalizing system normalizers introduced by Carter in (1), while Theorem 2 shows the same is true for A -groups (soluble groups with Abelian Sylow subgroups investigated by Taunt in (5)).
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 62 , Issue 3 , July 1966 , pp. 339 - 346
- Copyright
- Copyright © Cambridge Philosophical Society 1966
References
REFERENCES
- 1
- Cited by


