No CrossRef data available.
A Note on Some Integrals Involving Bessel Functions
Published online by Cambridge University Press: 24 October 2008
Extract
The object of this note is to prove the following results, all of which hold when |a| < 1.
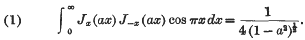
(2) If r is any positive integer other than zero, the
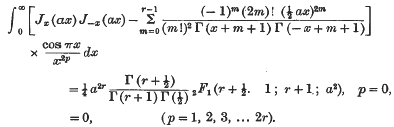
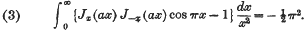
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 25 , Issue 2 , April 1929 , pp. 130 - 131
- Copyright
- Copyright © Cambridge Philosophical Society 1929
References
* Equations (1) and (3) were suggested for positive values of a(0<a<l) by some theorems of mine in null series (Proc. London Math. Soc. (2), 26 (1927), p. 54, Theorems 2 and 3). These theorems can be applied to transform Kapteyn series into integrals, but the proofs are very elaborate. For the proof below I am very much indebted to the referee. Apart from its simplicity it is true for complex values of a in the more extensive region |a| < 1.Google Scholar
† Watson, , Theory of Bessel Functions, p. 147 (5).Google Scholar
* Bromwich, , Theory of infinite series, 2nd Ed., p. 500, Theorem B.Google Scholar


