Published online by Cambridge University Press: 24 October 2008
Complex (associative) H*-algebras were introduced and studied in detail by Ambrose[1]; it was proved that every complex H*-algebra with zero annihilator is the l2-sum of a suitable family of topologically simple complex H*-algebras and that the H*-algebras 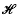
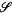 (H) of all Hilbert-Schmidt operators on any complex Hilbert space H are the only topologically simple complex H*-algebras. In a recent paper [2] Balachandran and Swaminathan observe that the reduction of the theory of real H*-algebras to the topologically simple case follows easily with minor changes of the complex argument, and they prove a theorem describing topologically simple real H*-algebras. This theorem can be equivalently reformulated as follows.
(H) of all Hilbert-Schmidt operators on any complex Hilbert space H are the only topologically simple complex H*-algebras. In a recent paper [2] Balachandran and Swaminathan observe that the reduction of the theory of real H*-algebras to the topologically simple case follows easily with minor changes of the complex argument, and they prove a theorem describing topologically simple real H*-algebras. This theorem can be equivalently reformulated as follows.