Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
DU, XIUMIN
GUTH, LARRY
LI, XIAOCHUN
and
ZHANG, RUIXIANG
2018.
POINTWISE CONVERGENCE OF SCHRÖDINGER SOLUTIONS AND MULTILINEAR REFINED STRICHARTZ ESTIMATES.
Forum of Mathematics, Sigma,
Vol. 6,
Issue. ,
Pierce, Lillian B
2020.
On Bourgain’s Counterexample for the Schrödinger Maximal Function.
The Quarterly Journal of Mathematics,
Vol. 71,
Issue. 4,
p.
1309.
Lee, Jungjin
2020.
Global Kato Type Smoothing Estimates via Local Ones for Dispersive Equations.
Journal of Fourier Analysis and Applications,
Vol. 26,
Issue. 1,
Compaan, Erin
Lucà, Renato
and
Staffilani, Gigliola
2020.
Pointwise Convergence of the Schrödinger Flow.
International Mathematics Research Notices,
Vol. 2021,
Issue. 1,
p.
596.
Li, Dan
Li, Junfeng
and
Xiao, Jie
2021.
An Upbound of Hausdorff’s Dimension of the Divergence Set of the Fractional SchröDinger Operator On Hs(ℝn).
Acta Mathematica Scientia,
Vol. 41,
Issue. 4,
p.
1223.
Li, Wenjuan
and
Wang, Huiju
2021.
A study on a class of generalized Schrödinger operators.
Journal of Functional Analysis,
Vol. 281,
Issue. 9,
p.
109203.
Yuan, Jiye
and
Zhao, Tengfei
2022.
Pointwise convergence along a tangential curve for the fractional Schrödinger equation with 0 < m < 1.
Mathematical Methods in the Applied Sciences,
Vol. 45,
Issue. 1,
p.
456.
Zhao, Yajuan
Yan, Xiangqian
Yan, Wei
and
Li, Yongsheng
2022.
Pointwise convergence problem of the Korteweg–de Vries–Benjamin–Ono equation.
Nonlinear Analysis: Real World Applications,
Vol. 67,
Issue. ,
p.
103611.
Zhao, Yajuan
Li, Yongsheng
Yan, Wei
and
Yan, Xiangqian
2022.
On the Dimension of the Divergence Set of the Ostrovsky Equation.
Acta Mathematica Scientia,
Vol. 42,
Issue. 4,
p.
1607.
Eceizabarrena, Daniel
and
Ponce-Vanegas, Felipe
2022.
Pointwise convergence over fractals for dispersive equations with homogeneous symbol.
Journal of Mathematical Analysis and Applications,
Vol. 515,
Issue. 1,
p.
126385.
Li, Wenjuan
Wang, Huiju
and
Xue, Qingying
2022.
A Survey on the Study of Generalized Schrödinger Operators along Curves.
Mathematics,
Vol. 11,
Issue. 1,
p.
8.
Yan, Wei
Wang, Weimin
and
Yan, Xiangqian
2022.
Convergence problem of the Kawahara equation on the real line.
Journal of Mathematical Analysis and Applications,
Vol. 515,
Issue. 1,
p.
126386.
Eceizabarrena, Daniel
and
Lucà, Renato
2022.
Convergence over fractals for the periodic
Schrödinger equation.
Analysis & PDE,
Vol. 15,
Issue. 7,
p.
1775.
Eceizabarrena, Daniel
and
Ponce-Vanegas, Felipe
2022.
Counterexamples for the fractal Schrödinger convergence problem with an Intermediate Space Trick.
Communications on Pure and Applied Analysis,
Vol. 21,
Issue. 11,
p.
3777.
Lucà, Renato
2022.
Qualitative Properties of Dispersive PDEs.
Vol. 52,
Issue. ,
p.
61.
Cho, Chu-Hee
and
Ko, Hyerim
2022.
Pointwise Convergence of the Fractional Schrödinger Equation in $\mathbb{R}^2$.
Taiwanese Journal of Mathematics,
Vol. 26,
Issue. 1,
Miao, Changxing
Yuan, Jiye
Zhao, Tengfei
and
Barron, Alex
2023.
Maximal estimates for Weyl sums on Td.
Journal of Functional Analysis,
Vol. 284,
Issue. 2,
p.
109747.
Chu, Rena
and
Pierce, Lillian B.
2023.
Generalizations of the Schrödinger maximal operator: building arithmetic counterexamples.
Journal d'Analyse Mathématique,
Vol. 151,
Issue. 1,
p.
59.
An, Chen
Chu, Rena
and
Pierce, Lillian B
2023.
Counterexamples for High-Degree Generalizations of the Schrödinger Maximal Operator.
International Mathematics Research Notices,
Vol. 2023,
Issue. 10,
p.
8371.
Li, Dan
and
Li, Jun Feng
2023.
A Carleson Problem for the Boussinesq Operator.
Acta Mathematica Sinica, English Series,
Vol. 39,
Issue. 1,
p.
119.
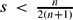 $s<\frac{n}{2(n+1)}$, for which the solution diverges on a set of nonzero Lebesgue measure. We provide a different example enabling the generalisation to fractional Hausdorff measure.
$s<\frac{n}{2(n+1)}$, for which the solution diverges on a set of nonzero Lebesgue measure. We provide a different example enabling the generalisation to fractional Hausdorff measure.