Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-26T08:38:02.475Z Has data issue: false hasContentIssue false
  • English
  • Français

A note on lemmas of Green and Kondo

Published online by Cambridge University Press:  24 October 2008

A. O. Morris
A. O. Morris
Affiliation:
University College of Wales, Aberystwyth
Get access Rights & Permissions [Opens in a new window]

Extract

Let R be the field of rational numbers, {x} = {x1, z2, …}, {y} = {y1, y2, …} be two countably infinite sets of variables and t an indeterminate. Let (λ) = (λ1, λ2, …, λm) be a partition of n. Then Littlewood (5) has shown that

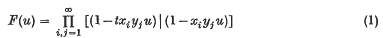
can be expressed in the form

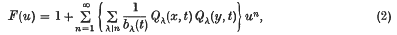
where Qλ(x, t) and Qλ(y, t) denote certain symmetric functions on the sets {x} and {y} respectively. In addition

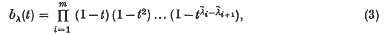
where 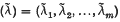is the partition of n conjugate to (λ). In fact, Littlewood (5) showed that

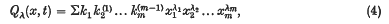
where the summation is over all terms obtained by permutations of the variables xi (i = 1, 2, …) and

.

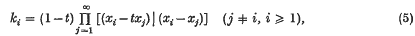
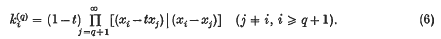Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 63 , Issue 1 , January 1967 , pp. 83 - 85
Copyright
Copyright © Cambridge Philosophical Society 1967

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Green, J. A.The characters of the finite general linear groups. Trans. Am. Math. Soc. 80 (1955), 402–47.CrossRefGoogle Scholar
(2)Green, J. A. Les polynomes de Hall et les caractères des groupes GL(n, q). Colloque d'algèbre supérieure, pp. 207–15 (Brussels, 1956).Google Scholar
(3)Kondo, T.On Gaussian sums attached to the general linear groups over finite fields. J. Math. Soc. Japan 15 (1963), 244–55.Google Scholar
(4)Littlewood, D. E.The theory of group characters and matrix representations of groups (Oxford, 1950).Google Scholar
(5)Littlewood, D. E.On certain symmetric functions. Proc. London Math. Soc. (3) 11 (1961), 485–98.CrossRefGoogle Scholar
(6)Morris, A. O.The multiplication of Hall Functions. Proc. London Math. Soc. (3) 13 (1963), 733–42.CrossRefGoogle Scholar
(7)Morris, A. O.The characters of the group GL(n, q). Math. Z. 81 (1963), 112–23.CrossRefGoogle Scholar