Published online by Cambridge University Press: 24 October 2008
The general construction of realizability toposes was first described in [3]. The data from which such a topos is constructed (called a partial applicative structure in [3]) consists of a set A equipped with a partial binary operation (called application and denoted by juxtaposition, with the convention that unbracketed expressions are evaluated from left to right) and two constants K, S satisfying
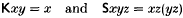
for all x, y, z ∈ A (where, as usual, an equality between possibly undefined terms means ‘one side is defined iff the other is, and then they are equal’). Following Lambek [6], we now call such a structure a partial Schönfinkel algebra, or a global Schönfinkel algebra if application is defined on the whole of A × A. (The name ‘combinatory algebra’ is also in common use.) We write 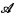 for the realizability topos constructed from A.
for the realizability topos constructed from A.