Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-26T13:22:05.908Z Has data issue: false hasContentIssue false
  • English
  • Français

A note on a theorem of Stanton-Weinstein on the L4-norm of spherical harmonics

Published online by Cambridge University Press:  24 October 2008

Jiang-Hua Lu
Jiang-Hua Lu
Affiliation:
Department of Mathematics, University of California, Berkeley, CA 94720, U.S.A.
Get access Rights & Permissions [Opens in a new window]

Extract

1. Let El (l = 0,1,2, …) be the eigenspaces of the Laplacian on the standard 2-sphere S2. Consider the function r2. 4: El −{0} → R given by

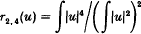
Stanton and Weinstein proved in [1] that r2, 4 was locally maximized by the ‘highest weight’ function 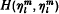. This note is to simplify part of their proof, namely that of the negativity of .

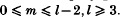Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 102 , Issue 3 , November 1987 , pp. 561 - 563
Copyright
Copyright © Cambridge Philosophical Society 1987

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCE

[1]Stanton, R. J. and Weinstein, A.. On the L 4 norm of spherical harmonics. Math. Proc. Cambridge Philos. Soc. 89 (1981), 343–358.CrossRefGoogle Scholar