Article contents
Multi-crossing number for knots and the Kauffman bracket polynomial
Published online by Cambridge University Press: 02 November 2016
Abstract
A multi-crossing (or n-crossing) is a singular point in a projection of a knot or link at which n strands cross so that each strand bisects the crossing. We generalise the classic result of Kauffman, Murasugi and Thistlethwaite relating the span of the bracket polynomial to the double-crossing number of a link, span〈K〉 ⩽ 4c2, to the n-crossing number. We find the following lower bound on the n-crossing number in terms of the span of the bracket polynomial for any n ⩾ 3:
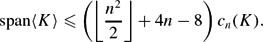 $$\text{span} \langle K \rangle \leq \left(\left\lfloor\frac{n^2}{2}\right\rfloor + 4n - 8\right) c_n(K).$$
$$\text{span} \langle K \rangle \leq \left(\left\lfloor\frac{n^2}{2}\right\rfloor + 4n - 8\right) c_n(K).$$
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 164 , Issue 1 , January 2018 , pp. 147 - 178
- Copyright
- Copyright © Cambridge Philosophical Society 2016
References
REFERENCES
- 7
- Cited by


