Hostname: page-component-669899f699-qzcqf Total loading time: 0 Render date: 2025-04-25T18:21:45.364Z Has data issue: false hasContentIssue false
  • English
  • Français

Minimum growth of harmonic functions and thinness of a set

Published online by Cambridge University Press:  24 October 2008

Jang-Mei G. Wu
Jang-Mei G. Wu
Affiliation:
University of Illinois, Urbana, IL 61801, U.S.A.
Get access Rights & Permissions [Opens in a new window]

Extract

In [3], Barth, Brannan and Hayman proved that if u(z) is any non-constant harmonic function in ℝ2, ø(r) is a positive increasing function of r for r ≥ 1 and

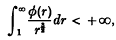
then there exists a path going from a finite point to ∞, such that u(z) > ø(|z|) on Γ. Moreover, they showed by example that the integral condition above cannot be relaxed.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 95 , Issue 1 , January 1984 , pp. 123 - 133
Copyright
Copyright © Cambridge Philosophical Society 1984

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

REFERENCES

[1] Ancona, A., Hayman, W. K. and Wu, J.-M.. The growth of harmonic functions along a path in space. J. London Math. Soc. (2), 24 (1981), 313–524.Google Scholar
[2] Arsove, M. and Huber, A.. Local behavior of subharmonic functions. Indiana Math. J. 22 (1973), 1191–1199.CrossRefGoogle Scholar
[3] Barth, K. F., Brannan, D. A. and Hayman, W. K.. The growth of plane harmonic functions along an asymptotic path. Proc. London Math. Soc. (3) 37 (1978), 363–384.CrossRefGoogle Scholar
[4] Cámera, G. A.. Minimum growth rate of subharmonic functions. Acta Cient. Venezolana 30 (1979), 349–359.Google Scholar
[5] Cámera, G. A.. Subharmonic functions on sets of finite measure. Quart. J. Math. Oxford (2), 33 (1982), 27–43.CrossRefGoogle Scholar
[6] Helms, L. L.. Introduction to Potential Theory (Wiley, 1969).Google Scholar
[7] Landkof, N. S.. Foundation of Modern Potential Theory (Springer-Verlag, 1972).CrossRefGoogle Scholar
[8] Tsuji, M.. Potential Theory in Modern Function Theory (Chelsea, 1975).Google Scholar