Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-19T03:48:23.124Z Has data issue: false hasContentIssue false
  • English
  • Français

Metric Diophantine approximation with two restricted variables I. Two square-free integers, or integers in arithmetic progressions

Published online by Cambridge University Press:  24 October 2008

Glyn Harman
Glyn Harman
Affiliation:
Department of Pure Mathematics, University College, Cardiff
Get access Rights & Permissions [Opens in a new window]

Extract

In this paper, together with [7] and [8], we shall be concerned with estimating the number of solutions of the inequality

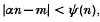
for almost all α (in the sense of Lebesgue measure on Iℝ), where 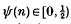, and both m and n are restricted to sets of number-theoretic interest. Our aim is to prove results analogous to the following theorem (an improvement given in [2] of an earlier result of Khintchine [10]) and its quantitative developments (for example, see [11, 12,6]):

Let ψ(n) be a non-increasing positive function of a positive integer variable n. Then the inequality (1·1) has infinitely many, or only finitely many, solutions in integers to, n(n > 0) for almost all real α, according to whether the sum

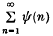
diverges, or converges, respectively.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 103 , Issue 2 , March 1988 , pp. 197 - 206
Copyright
Copyright © Cambridge Philosophical Society 1988

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Cassels, J. W. S.. Some metrical theorems in Diophantine approximation I. Proc. Cambridge Philos. Soc. 46 (1950), 209–218.CrossRefGoogle Scholar
[2]Duffin, R. J. and Schaeffer, A. C.. Khintchine's problem in metric Diophantine approximation. Duke Math. J. 8 (1941), 243–255.CrossRefGoogle Scholar
[3]Erdös, P.. On the distribution of the convergents of almost all real numbers. J. Number Theory 2 (1970), 425–441.CrossRefGoogle Scholar
[4]Hardy, G. H. and Wright, E. M.. An Introduction to the Theory of Numbers, 5th ed. (Oxford University Press, 1979).Google Scholar
[5]Harman, G.. Diophantine approximation with square-free integers. Math. Proc. Cambridge Philos. Soc. 95 (1984), 381–388.CrossRefGoogle Scholar
[6]Harman, G.. Some theorems in the metric theory of Diophantine approximation. Math. Proc. Cambridge Philos. Soc. 99 (1986), 385–394.CrossRefGoogle Scholar
[7]Harman, G.. Metric Diophantine approximation with two restricted variables. II: a prime and a square-free. Mathematika, to appear.Google Scholar
[8]Harman, G.. Metric Diophantine approximation with two restricted variables. III: two prime numbers. Preprint, University College, Cardiff (1986).Google Scholar
[9]Heath-Brown, D. R.. Diophantine approximation with square-free integers. Math. Z. 187 (1984), 335–344.CrossRefGoogle Scholar
[10]Khintchine, A.. Einige Sätze über Kettenbrüche, mit Anwendungen auf die Theorie der Diophantischen Approximationen. Math. Ann. 92 (1924), 115–125.CrossRefGoogle Scholar
[11]Leveque, W. J.. On the frequency of small fractional parts in certain real sequences III. J. Reine Angew. Math. 202 (1959), 215–220.CrossRefGoogle Scholar
[12]Schmidt, W. M.. Metrical theorems on fractional parts of sequences. Trans. Amer. Math. Soc. 110, (1964), 493–518.CrossRefGoogle Scholar
[13]Sprindzuk, V. G.. Metric Theory of Diophantine Approximation, translated by R. A. Silverman (Winston/Wiley, 1979).Google Scholar
[14]Szüsz, P.. Über die metrische theorie der Diophantischen Approximation II. Acta Arith. 8, (1962/1963), 225–241.CrossRefGoogle Scholar
[15]Vaaler, J. D.. On the metric theory of Diophantine approximation. Pacific J. Math. (1978), 527–539.CrossRefGoogle Scholar