Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-30T00:10:55.506Z Has data issue: false hasContentIssue false
  • English
  • Français

A measure of dispersion applied to cosmic-ray and other problems

Published online by Cambridge University Press:  24 October 2008

S. R. Broadbent
S. R. Broadbent
Affiliation:
British Coal Utilisation Research AssociationLeatherhead
Get access Rights & Permissions [Opens in a new window]

Abstract

The statistic 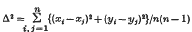is applied in several different situations to detect departure from uniform dispersion. The given sample points may lie on a square lattice (without repetition), a rectangular lattice (repetition being allowed), or within rectangular or circular plane boundaries. The problems considered include an analysis of cosmic ray shower structure, and the counting of dust particles and bacterial colonies.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 52 , Issue 3 , July 1956 , pp. 499 - 513
Copyright
Copyright © Cambridge Philosophical Society 1956

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Cramér, H.Mathematical methods of statistics (Princeton, 1946).Google Scholar
(2)Cranshaw, T. E. and Galbraith, W.Time variations of extensive air showers and the origin of cosmic rays. Phil. Mag. (7), 45 (1954), 1109–18.Google Scholar
(3)Feller, W.Probability theory and its applications, vol. 1 (New York, 1950).Google Scholar
(4)Fisher, R. A.Statistical methods for research workers, 10th ed. (London, 1946).Google Scholar
(5)Fisher, R. A.The significance of deviations from expectation in a Poisson series. Biometrics, 6 (1950), 17–24.CrossRefGoogle Scholar
(6)Gini, C.Studi economico-giuridici delta R. Università di Cagliari, 3 (2) (1912), 80.Google Scholar
(7)Iyer, P. V. Krishna.The first and second moments of some probability distributions arising from points on a lattice and their applications. Biometrika, 36 (1949), 135–41.Google Scholar
(8)Kendall, M. G.The advanced theory of statistics, vol. 1, 2nd ed. (London, 1945).Google Scholar
(9)Molière, G.Cosmic rays (New York, 1945).Google Scholar
(10)Moran, P. A. P.Random associations on a lattice. Proc. Camb. phil. Soc. 43 (1947), 327.CrossRefGoogle Scholar
(11)Neyman, J.Lectures and conferences on mathematical statistics and probability, 2nd ed. (Department of Agriculture, Washington, 1952).Google Scholar
(12)Patnaik, P. B.The non-central X2 and F distributions and their applications. Biometrika, 36 (1949), 202–32.Google Scholar
(13)Pearson, E. S. and Hartley, H. O.Charts of the power function for analysis of variance tests, derived from the non-central F-distribution. Biometrika, 38 (1951), 112–30.CrossRefGoogle ScholarPubMed
(14)Williams, R. W.The structure of the large cosmic ray showers. Phys. Rev. (2), 74 (1948), 1689–707.CrossRefGoogle Scholar
(15)Williamson, B.An elementary treatise on the integral calculus, 3rd ed. (London, 1880).Google Scholar