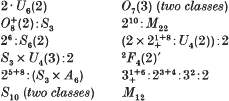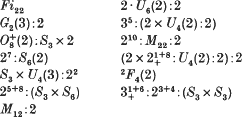Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Moori, Jamshid
1994.
(2,3,p)-generations for the fischer group f22.
Communications in Algebra,
Vol. 22,
Issue. 11,
p.
4597.
Rowley, Peter
and
Walker, Louise
1994.
A note on the 𝑀₂₃- and 𝐹𝑖₂₃-minimal parabolic geometries.
Proceedings of the American Mathematical Society,
Vol. 121,
Issue. 2,
p.
317.
Moori, Jamshid
1994.
SUBGROUPS OF 3-TRANSPOSITION GROUPS GENERATED BY FOUR 3-TRANSPOSITIONS.
Quaestiones Mathematicae,
Vol. 17,
Issue. 1,
p.
83.
Linton, Stephen A.
Lux, Klaus
and
Soicher, Leonard H.
1995.
The Primitive Distance-Transitive Representations of the Fischer Groups.
Experimental Mathematics,
Vol. 4,
Issue. 3,
p.
235.
Liebeck, Martin W.
Praeger, Cheryl E.
and
Saxl, Jan
2000.
Transitive Subgroups of Primitive Permutation Groups.
Journal of Algebra,
Vol. 234,
Issue. 2,
p.
291.
O’Reilly Regueiro, Eugenia
2005.
Biplanes with flag-transitive automorphism groups of almost simple type, with alternating or sporadic socle.
European Journal of Combinatorics,
Vol. 26,
Issue. 5,
p.
577.
Cossidente, Antonio
and
King, Oliver H.
2008.
On the geometry of the exceptional group G 2(q), q even.
Designs, Codes and Cryptography,
Vol. 47,
Issue. 1-3,
p.
145.
Zhou, ShengLin
and
Dong, HuiLi
2009.
Sporadic groups and flag-transitive triplanes.
Science in China Series A: Mathematics,
Vol. 52,
Issue. 2,
p.
394.
Konygin, A. V.
2011.
On primitive permutation groups with a stabilizer of two points that is normal in the stabilizer of one of them: Case when the socle is a power of a sporadic simple group.
Proceedings of the Steklov Institute of Mathematics,
Vol. 272,
Issue. S1,
p.
65.
Pellegrini, M.A.
Tamburini Bellani, M.C.
and
Vsemirnov, M.A.
2012.
Uniform (2,k)-generation of the 4-dimensional classical groups.
Journal of Algebra,
Vol. 369,
Issue. ,
p.
322.
Ali, Faryad
2014.
On the ranks ofFi22.
Quaestiones Mathematicae,
Vol. 37,
Issue. 4,
p.
591.
Tamburini Bellani, M. Chiara
and
Vsemirnov, Maxim
2015.
Hurwitz Generation of PSp6(q).
Communications in Algebra,
Vol. 43,
Issue. 10,
p.
4159.
LUCCHINI, ANDREA
MARION, CLAUDE
and
TRACEY, GARETH
2020.
GENERATING MAXIMAL SUBGROUPS OF FINITE ALMOST SIMPLE GROUPS.
Forum of Mathematics, Sigma,
Vol. 8,
Issue. ,
Craven, David A.
2023.
The maximal subgroups of the exceptional groups $F_{4}(q)$, $E_{6}(q)$ and $^{2}\!E_{6}(q)$ and related almost simple groups.
Inventiones mathematicae,
Vol. 234,
Issue. 2,
p.
637.
Trofimov, V. I.
2023.
A Graph with a Locally Projective Vertex-Transitive Group of Automorphisms Aut($$Fi_{22}$$) Which Has a Nontrivial Stabilizer of a Ball of Radius $$2$$.
Proceedings of the Steklov Institute of Mathematics,
Vol. 323,
Issue. S1,
p.
S300.
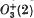 ) should read
) should read 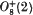 .) More precisely, we prove
.) More precisely, we prove