Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Ershov, Yu. L.
1989.
Invariant generation.
Siberian Mathematical Journal,
Vol. 29,
Issue. 5,
p.
775.
Herfort, Wolfgang N.
and
Ribes, Luis
1989.
Frobenius subgroups of free products of prosolvable groups.
Monatshefte f�r Mathematik,
Vol. 108,
Issue. 2-3,
p.
165.
Geyer, W. D.
and
Jarden, M.
1991.
The Henselian closures of a PpC field.
Abhandlungen aus dem Mathematischen Seminar der Universität Hamburg,
Vol. 61,
Issue. 1,
p.
63.
Jarden, Moshe
1991.
Generators and Relations in Groups and Geometries.
p.
343.
Mel'nikov, O. V.
1999.
On free products of absolute Galois groups.
Siberian Mathematical Journal,
Vol. 40,
Issue. 1,
p.
95.
Bary-Soroker, Lior
2010.
Projective pairs of profinite groups.
Journal of Algebra,
Vol. 324,
Issue. 9,
p.
2112.
Ribes, Luis
2017.
Profinite Graphs and Groups.
Vol. 66,
Issue. ,
p.
177.
Breuer, Thomas
and
Guralnick, Robert M.
2023.
Finite groups can be generated by a π-subgroup and a π′-subgroup.
Israel Journal of Mathematics,
Vol. 257,
Issue. 1,
p.
56.


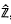 , the profinite completion of
, the profinite completion of