Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-26T07:46:48.785Z Has data issue: false hasContentIssue false
  • English
  • Français

A Matrix Factorization Problem in the Theory of Random Variables Defined on a Finite Markov Chain

Published online by Cambridge University Press:  24 October 2008

H. D. Miller
H. D. Miller
Affiliation:
Statistical LaboratoryUniversity of Cambridge
Get access Rights & Permissions [Opens in a new window]

Summary

Let {kr} (r = 0, 1, 2, …; 1 ≤ kr ≤ h) be a positively regular, finite Markov chain with transition matrix P = (pjk). For each possible transition j → k let gjk(x)(− ∞ ≤ x ≤ ∞) be a given distribution function. The sequence of random variables {ξr} is defined where ξr has the distribution gjk(x) if the rth transition takes the chain from state j to state k. 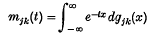It is supposed that each distribution gjk(x) admits a two-sided Laplace-Stieltjes transform in a real t-interval surrounding t = 0. Let P(t) denote the matrix {Pjkmjk(t)}. It is shown, using probability arguments, that I − sP(t) admits a Wiener-Hopf type of factorization in two ways 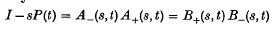for suitable values of s where the plus-factors are non-singular, bounded and have regular elements in a right half of the complex t-plane and the minus-factors have similar properties in an overlapping left half-plane (Theorem 1).

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 58 , Issue 2 , April 1962 , pp. 268 - 285
Copyright
Copyright © Cambridge Philosophical Society 1962

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Craméer, H.On some questions connected with mathematical risk. Univ. California Publ. Statist. 2 (1954), 99–124.Google Scholar
(2)Debreu, G. and Herstein, I. NNon-negative square matrices. Econometrica, 21 (1953), 597–607.CrossRefGoogle Scholar
(3)Kemperman, J. H. B.The passage problem for a stationary Markov chain (Chicago, 1961).CrossRefGoogle Scholar
(4)Masani, P.The Laurent factorization of operator-valued functions. Proc. London Math. Soc. (3), 6 (1956), 56–69.Google Scholar
(5)Miller, H. DAbsorption probabilities for sums of random variables defined on a finite Markov chain. Proc. Cambridge Philos. Soc.58 (1962), 286–298.CrossRefGoogle Scholar
(6)Miller, H. DA generalization of Wald's identity with applications to random walks. Ann. Math. Statist.32 (1961), 549–560.CrossRefGoogle Scholar
(7)Miller, H. DA convexity property in the theory of random variables defined on a finite Markov chain. Ann. Math. Statist.32 (1961), 1260–1270.CrossRefGoogle Scholar
(8)Spitzer, F.A Tauberian theorem and its probability interpretation. Trans. American Math. Soc.94 (1960), 150–169.CrossRefGoogle Scholar
(9)Widder, D. VThe Laplace transform (Princeton, 1946).Google Scholar
(10)Wiener, N. and Masani, P.The prediction theory of multivariate stochastic processes. II. Acta Math.99 (1958), 93–137.CrossRefGoogle Scholar
(11)Yaglom, A. MEffective solutions of linear approximation problems for multivariate stationary processes with a rational spectrum. Teor. Veroyatnost. i Primenen. 5 (1960), 265–292. (In Russian.)Google Scholar