Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Sendov, Bl.
2016.
Geometric relations between the zeros of polynomials.
Proceedings of the Steklov Institute of Mathematics,
Vol. 293,
Issue. 1,
p.
317.
Sendov, Blagovest
and
Sendov, Hristo
2017.
Progress in Approximation Theory and Applicable Complex Analysis.
Vol. 117,
Issue. ,
p.
145.
SENDOV, BLAGOVEST
and
SENDOV, HRISTO
2019.
Duality between loci of complex polynomials and the zeros of polar derivatives.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 167,
Issue. 01,
p.
65.
Sendov, Hristo
and
Xiao, Junquan
2021.
On loci of complex polynomials of degree three.
Journal of Mathematical Analysis and Applications,
Vol. 495,
Issue. 2,
p.
124767.
Gardner, Robert B.
Govil, Narendra K.
Milovanović, Gradimir V.
and
Rassias, Themistocles M.
2022.
Extremal Problems and Inequalities of Markov-Bernstein Type for Algebraic Polynomial.
p.
329.
2022.
Extremal Problems and Inequalities of Markov-Bernstein Type for Algebraic Polynomial.
p.
391.
Sendov, Hristo
and
Xiao, Junquan
2023.
Complex multi-affine polynomials and invariant circles.
Journal of Mathematical Analysis and Applications,
Vol. 523,
Issue. 2,
p.
127076.
Sendov, Hristo
and
Xiao, Junquan
2023.
Coninvolutory matrices, multi-affine polynomials, and invariant circles.
Linear and Multilinear Algebra,
Vol. 71,
Issue. 6,
p.
911.
Sendov, Hristo
and
Xiao, Junquan
2024.
On the Geometry of Multi-affine Polynomials: Invariant Circles and Circular Solutions.
Computational Methods and Function Theory,
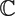 ${\mathbb C}$* is a locus of p(z) if it contains a zero of any of its apolar polynomials and is the smallest such set with respect to inclusion. Using the notion locus, some classical theorems in the geometry of polynomials can be refined. We show that each locus is a Lebesgue measurable set and investigate its intriguing connections with the higher-order polar derivatives of p.
${\mathbb C}$* is a locus of p(z) if it contains a zero of any of its apolar polynomials and is the smallest such set with respect to inclusion. Using the notion locus, some classical theorems in the geometry of polynomials can be refined. We show that each locus is a Lebesgue measurable set and investigate its intriguing connections with the higher-order polar derivatives of p.