Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-29T19:27:33.473Z Has data issue: false hasContentIssue false
  • English
  • Français

Links with super-additive tunnel number

Published online by Cambridge University Press:  24 October 2008

Michel Boileau ,
Martin Lustig  and
Yoav Moriah
Michel Boileau
Affiliation:
Université Paul Sabatier, Département de Mathématiques, 118 route de Narbonne, 31062 Toulouse, France
Martin Lustig
Affiliation:
Institut für Mathematik, Ruhr-Universität Bochum, Postfach 10 21 48, 4630 Bochum 1, Germany
Yoav Moriah
Affiliation:
Department of Mathematics, Technion, Haifa 32000, Israel
Get access Rights & Permissions [Opens in a new window]

Extract

Let L ⊂ S3 be a knot or a link. A tunnel system for L is a collection of disjoint arcs t1, … ts properly embedded in S3−N(L) so that 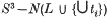is a handlebody. Alternatively one can view the t1, … ts ascocores of 2-handles which have to be attached to a handlebody in order to obtain S3−N(L). It follows immediately that this handlebody is of genus s+1. The tunnel number of L, denoted by t(L), is defined to be the minimal cardinality of all such collections.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 115 , Issue 1 , January 1994 , pp. 85 - 95
Copyright
Copyright © Cambridge Philosophical Society 1994

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Birman, J. and Hilden, H.. The homeomorphism problem for S 3. Bull. Amer. Math. Soc. 79 (1973), 1006–1010.CrossRefGoogle Scholar
[2]Doll, H.. Generalized bridge number for links in 3-manifolds, preprint 1991.CrossRefGoogle Scholar
[3]Gonzáles-Acuñna, F. and Short, H.. Knot surgery and primeness. Math. Proc. Cambridge Philos. Soc. 99 (1986), 89–102.CrossRefGoogle Scholar
[4]Jaco, W.. Lectures on three-manifold topology. Regional conf. series in math. 43, A.M.S. 1980.CrossRefGoogle Scholar
[5]Lustig, M.. On the Rank, the Deficiency and the Hcmological Dimension of Groups: The Computation of a Lower Bound via Fox Ideals, in Topology and Combinatorial Group Theory, Latiolais, P. (ed.), Lecture Notes in Mathematics 1440, 164–174. (Springer Verlag, 1991.)Google Scholar
[6]Lustig, M. and Moriah, Y.. Generating Systems for Groups and Reidemeister–Whitehead Torsion, to appear in J. of Algebra.Google Scholar
[7]Lustig, M. and Moriah, Y.. Generalized Montesinos Knots, Tunnels and N-Torsion, to appear in Math. Annalen.Google Scholar
[8]Montesinos, J.. Surgery on links and double branched coverings of S 3, in Knots, Groups, and 3-Manifolds, Neurwith, L. P. (ed.), Annals of Math. Studies 84 227–260 (Princeton University Press 1975).CrossRefGoogle Scholar
[9]Morimoto, K.. On behavior of tunnel number of knots under connected sum, preprint 1992.Google Scholar
[10]Norwood, F.. Every two-generator knot is prime. Proc. A.M.S. 86 (1982), 143–147.CrossRefGoogle Scholar
[11]Viro, O.. Linkings, 2-sheeted branched coverings and braids. Math. USSR Sbornik 16 (1972), 223–226.CrossRefGoogle Scholar