No CrossRef data available.
Published online by Cambridge University Press: 24 October 2008
§ 1. “Stretches” joining Points in a Metrical Space.
If x, y, z are any points in a metrical space, then by definition
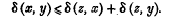
Regarding x and y as fixed, we may define the set of points z for which
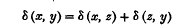
as the “stretch joining the points xy” or more shortly the stretch xy*. Then for points z not on the stretch,
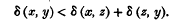
The stretch xy always contains the points x and y themselves, which we may call the “end-points” of the stretch. In particular cases, it may contain no other points: e.g. with the function δ0(x, y) = 1 when xǂy, each stretch contains only its end-points †.
* See Menger, , “Ueber geodätische Linien in allgemeinen metrischen Ränmen,” Amsterdam Proceedings, Vol. xxix (1926), p. 166.Google Scholar
† If each stretch contains at least one" point in addition to its end-points, the space is said to be “convex.” See Menger, op. cit.