(LF)-spaces with absolute bases
Published online by Cambridge University Press: 24 October 2008
Extract
Suppose E is a locally convex space over a field K which can be the real line or the complex plane. Then a basis for E is a sequence (xk) of elements of E such that, if x ∈ E, x can be expressed uniquely as
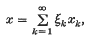
where ξk ∈K for each k. If this representation converges absolutely, i.e. if
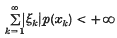
for every continuous seminorm p on E, then (xk) is called an absolute basis for E. If the mappings x → ξk from E into K are continuous for each k, then (xk) is a Schauder basis for E. The purpose of this paper is to prove some results for (LF)-spaces with bases and to use them to extend some theorems due to Pietsch. We recall that an (F)-space is a complete metrizable locally convex space and an (LF)-space the inductive limit of a strictly increasing sequence of (F)-spaces (En, τn) such that τn+1|En = τn for all n.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 67 , Issue 2 , March 1970 , pp. 283 - 286
- Copyright
- Copyright © Cambridge Philosophical Society 1970
References
REFERENCES
- 1
- Cited by


