Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-26T11:30:08.521Z Has data issue: false hasContentIssue false
  • English
  • Français

Leading terms of Artin L-series at negative integers and annihilation of higher K-groups

Published online by Cambridge University Press:  27 April 2011

ANDREAS NICKEL
ANDREAS NICKEL*
Affiliation:
Universität Regensburg, Fakultät für Mathematik, Universitätsstr. 31, 93053 Regensburg, Germany. e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let L/K be a finite Galois extension of number fields with Galois group G. We use leading terms of Artin L-series at strictly negative integers to construct elements which we conjecture to lie in the annihilator ideal associated to the Galois action on the higher dimensional algebraic K-groups of the ring of integers in L. For abelian G our conjecture coincides with a conjecture of Snaith and thus generalizes also the well-known Coates–Sinnott conjecture. We show that our conjecture is implied by the appropriate special case of the equivariant Tamagawa number conjecture (ETNC) provided that the Quillen–Lichtenbaum conjecture holds. Moreover, we prove induction results for the ETNC in the case of Tate motives h0(Spec(L))(r), where r is a strictly negative integer. In particular, this implies the ETNC for the pair (h0(Spec(L))(r), 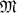), where L is totally real, r < 0 is odd and 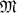is a maximal order containing ℤ[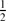]G, and will also provide some evidence for our conjecture.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 151 , Issue 1 , July 2011 , pp. 1 - 22
Copyright
Copyright © Cambridge Philosophical Society 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[Ba77]Barsky, D. Fonctions zêta p-adique d'une classe de rayon des corps de nombres totalement réels. Groupe d'Etude d'Analyse Ultramétrique (1977/78), Exp. No. 16.Google Scholar
[BN02]Benois, D. and Nguyen Quang Do, T.Les nombres de Tamagawa locaux et la conjecture de Bloch et Kato pour les motifs ℚ(m) sur un corps abélien. Ann. Sci. Éc Norm. Sup. (4) 35 (2002), 641–672.Google Scholar
[Bo74]Borel, A.Stable real cohomology of arithmetic groups. Ann. Sci. Éc Norm. Sup. 7 (1974), 235–272.CrossRefGoogle Scholar
[Bo77]Borel, A.Cohomologie de SL n et valeurs de fonctions zêta aux points entiers. Ann. Sci. Norm. Sup. Pisa 4 (1977), 613–636.Google Scholar
[BS10]Buckingham, P. and Snaith, V. P.Functoriality of the canonical fractional Galois ideal. Canad. J. Math. 62 (2010), 1011–1036.CrossRefGoogle Scholar
[BG02]Burgos Gil, J. I.The regulators of Beilinson and Borel. CRM Monogr. Series 15 Amer Math. Soc. (2002).Google Scholar
[Bu03]Burns, D.Equivariant Whitehead torsion and refined euler characteristics. CRM Proc. Lect. Notes 36 (2003), 35–59.Google Scholar
[Bu08]Burns, D.On refined Stark conjectures in the non-abelian case. Math. Res. Lett. 15 (2008), 841–856.CrossRefGoogle Scholar
[Bu10]Burns, D.On leading terms and values of equivariant motivic L-functions. Pure Appl. Math. Q. 6 (1) (2010), 83–171.Google Scholar
[Bu]Burns, D. On main conjectures in non-commutative Iwasawa theory and related conjectures, preprint - see http://www.mth.kcl.ac.uk/staff/dj_burns/newdbpublist.html.Google Scholar
[BdJG]Burns, D., de Jeu, R. and Gangl, H. On special elements in higher algebraic K-theory and the Lichtenbaum–Gross conjecture, preprint - see http://www.mth.kcl.ac.uk/staff/dj_burns/newdbpublist.html.Google Scholar
[BF01]Burns, D. and Flach, M.Tamagawa numbers for motives with (non-commutative) coefficients, Doc. Math. 6 (2001), 501–570.CrossRefGoogle Scholar
[BF98]Burns, D. and Flach, M.On Galois structure invariants associated to Tate motives. Amer. J. Math. 120 (1998), 1343–1397.CrossRefGoogle Scholar
[BG03a]Burns, D. and Greither, C.On the equivariant Tamagawa number conjecture for Tate motives. Invent. Math. 153 (2003), 305–359.CrossRefGoogle Scholar
[BG03b]Burns, D. and Greither, C. Equivariant Weierstrass preparation and values of L-functions at negative integers. Doc. Math., J. DMV Extra Vol. (2003), 157–185.CrossRefGoogle Scholar
[Ca79]Cassou-Noguès, P.Valeurs aux entiers négatifs des fonctions zêta et fonctions zêta p-adiques. Invent. Math. 51 (1979), 29–59.Google Scholar
[CKPS98]Chinburg, T., Kolster, M., Pappas, G. and Snaith, V. Galois structure of K-groups of rings of integers, K-theory 14 (1998), 319–369.Google Scholar
[Co77]Coates, J.p-adic L-functions and Iwasawa's theory. Algebr. Number Fields (Proc. Symp. London math. Soc., University Durham 1975) (1977), 269–353.Google Scholar
[CS74]Coates, J. and Sinnott, W.An analogue of Stickelberger's theorem for the higher K-groups. Invent. Math. 25 (1974), 253–279.CrossRefGoogle Scholar
[CR87]Curtis, C. and Reiner, W. I.Methods of Representation Theory with Applications to Finite groups and orders, Vol. 2 (John Wiley & Sons, 1987).Google Scholar
[DR80]Deligne, P. and Ribet, K.Values of abelian L-functions at negative integers over totally real fields. Invent. Math. 59 (1980), 227–286.Google Scholar
[DF85]Dwyer, W. and Friedlander, E.Algebraic and étale K-theory, Trans. Amer. Math. Soc. 292 (1985), 247–280.Google Scholar
[FW79]Ferrero, B. and Washington, L.The Iwasawa invariant μp vanishes for abelian number fields. Ann. Math. 109 (1979), 377–395.CrossRefGoogle Scholar
[Gr05]Gross, B.H.On the values of Artin L-functions. Pure Appl. Math. Q. 1 (1) (2005), 1–13.CrossRefGoogle Scholar
[HK03]Huber, A. and Kings, G.Bloch–Kato conjecture and main conjecture of Iwasawa theory for Dirichlet characters, Duke Math. J. 119 (2003), 393–464.Google Scholar
[Ko03]Kolster, M.K-theory and arithmetic, in Karoubi, M. et al. (ed.), Contemporary developments in algebraic K-theory, Proceedings of the School and Conference on Algebraic K-theory and its Applications, ICTP (Trieste, Italy, July 8–19, 2002), ICTP Lecture Notes 15 (2003), 195–258.Google Scholar
[KNF96]Kolster, M., Nguyen Quang Do, T. and Fleckinger, V.Twisted S-units, p-adic class number formulas, and the Lichtenbaum conjectures. Duke Math. J. 84 (1996), 679–717; Correction, Duke Math. J. 90 (1997), 641–643.CrossRefGoogle Scholar
[NSW00]Neukirch, J., Schmidt, A. and Wingberg, K.Cohomology of Number Fields (Springer, 2000).Google Scholar
[Ng05]Nguyen Quang Do, T.Conjecture principale équivariante, idéaux de Fitting et annulateurs en théorie d'Iwasawa J. Théor. Nombres Bordeaux 17 (2005), 643–668.CrossRefGoogle Scholar
[Nia]Nickel, A. On the equivariant Tamagawa number conjecture in tame CM-extensions. To appear in Math. Z. (2010), DOI 10.1007/s00209-009-0658-9.Google Scholar
[Ni10]Nickel, A.Non-commutative Fitting invariants and annihilation of class groups. J. Algebra 323 (10) (2010), 2756–2778.CrossRefGoogle Scholar
[Po09]Popescu, C. D.On the Coates-Sinnott conjecture. Math. Nachr. 282 (10) (2009), 1370–1390.Google Scholar
[RW97]Ritter, J. and Weiss, A.Cohomology of units and L-values at zero. J. Amer. Math. Soc. 10 (1997), 513–552.CrossRefGoogle Scholar
[Si70]Siegel, C. L. Über die Fourierschen Koeffizienten von Modulformen. Nachr. Akad. Wiss. Gött., II. Math.-Phys. Kl. (1970), 15–56.Google Scholar
[So79]Soulé, C.K-théorie des annaux d'entier de corps de nombres et cohomologie étale. Invent. Math. 55 (3) (1979), 251–295.CrossRefGoogle Scholar
[Sn06]Snaith, V. P.Stark's conjecture and new Stickelberger phenomena, Canad. J. Math. 58 (2) (2006), 419–448.Google Scholar
[Ta84]Tate, J.Les conjectures de Stark sur les fonctions L d'Artin en s=0 (Birkhäuser, 1984).Google Scholar
[Wi90]Wiles, A.The Iwasawa conjecture for totally real fields. Ann. Math. 131, 493–540 (1990).CrossRefGoogle Scholar