Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-28T14:36:30.893Z Has data issue: false hasContentIssue false
  • English
  • Français

The lattice properties of asymmetric hyperbolic regions

III. a further result

Published online by Cambridge University Press:  24 October 2008

J. W. S. Cassels
J. W. S. Cassels
Affiliation:
Trinity CollegeCambridge
Get access Rights & Permissions [Opens in a new window]

Extract

1. Let

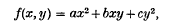
where a > 0, be an indefinite quadratic form, so that d = b2 − 4ac > 0. A classical theorem of Minkowski states that, if (x0, y0) is any pair of real numbers, there are numbers (x, y) congruent (mod 1) to (x0, y0), such that

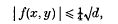
and, more recently, Davenport has shown that this theorem can be sharpened for certain special f, for instance that it is always possible to satisfy

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 44 , Issue 4 , October 1948 , pp. 457 - 462
Copyright
Copyright © Cambridge Philosophical Society 1948

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

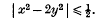
† Davenport, , Proc. K. Ned. Akad. Wet. Amsterdam, 44 (1946), 815–21.Google Scholar

‡ Remak, , Jber. dtsch. MatVer. 44 (1934), 238–49.Google Scholar

§ This f(x, y) plays a special part in another lattice problem. See Segre, , Duke Math. J. (1945), 337–65.CrossRefGoogle Scholar

† See Fig. 1.

† To justify (3) a postiori we note the identity, which can be proved directly,

where ξ = 2as 1x + b(x + s 1y) + 2cy − f (s 11) and η = y − ½. The origin and (s 1, 1) correspond to ±(f(s 1, 1), ½) in (ξ, η) coordinates so that at the intersections ξ = 0, and f(x, y) = f(x − s 1,y − 1) = ¼e.

‡ See Fig. 2. The region ℒ is enclosed by the dense line.