Article contents
Landau damping for non-Maxwellian distributions
Published online by Cambridge University Press: 24 October 2008
Abstract
It has been shown by Landau(8) that in a uniform plasma with a Maxwelliau velocity distribution longitudinal waves are damped. Penrose(9) has considered more general distributions and developed stability criteria. In particular, if the velocity distribution function has only one maximum, then the plasma is stable. In this paper the values of the Landau damping for some stable single maximum distributions are compared in order to assess the sensitivity of Landau damping to the form of the distribution function, and to investigate the usefulness of approximating to the Landau damping in a Maxwellian plasma by using an algebraically simpler velocity distribution function.
It is shown also that, for at least some velocity distributions having a maximum particle velocity, the behaviour of the plasma can no longer be described in terms of exponential damping, since there will be longer lasting perturbations with phase velocity equal to the maximum particle velocity.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 58 , Issue 1 , January 1962 , pp. 119 - 129
- Copyright
- Copyright © Cambridge Philosophical Society 1962
References
REFERENCES
- 8
- Cited by


 in a complex region (Moscow,
in a complex region (Moscow, 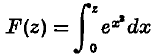 in a complex region (Moscow,
in a complex region (Moscow, 